The area of the region described by A={(x,y):x2+y2≤1andy2≤1−x} is
A
π2−23
B
π2+23
C
π2+43
D
π2−43
Video Solution
Text Solution
The correct Answer is:C
Clearly, Required area=Area of the circle -Area of the shaded region
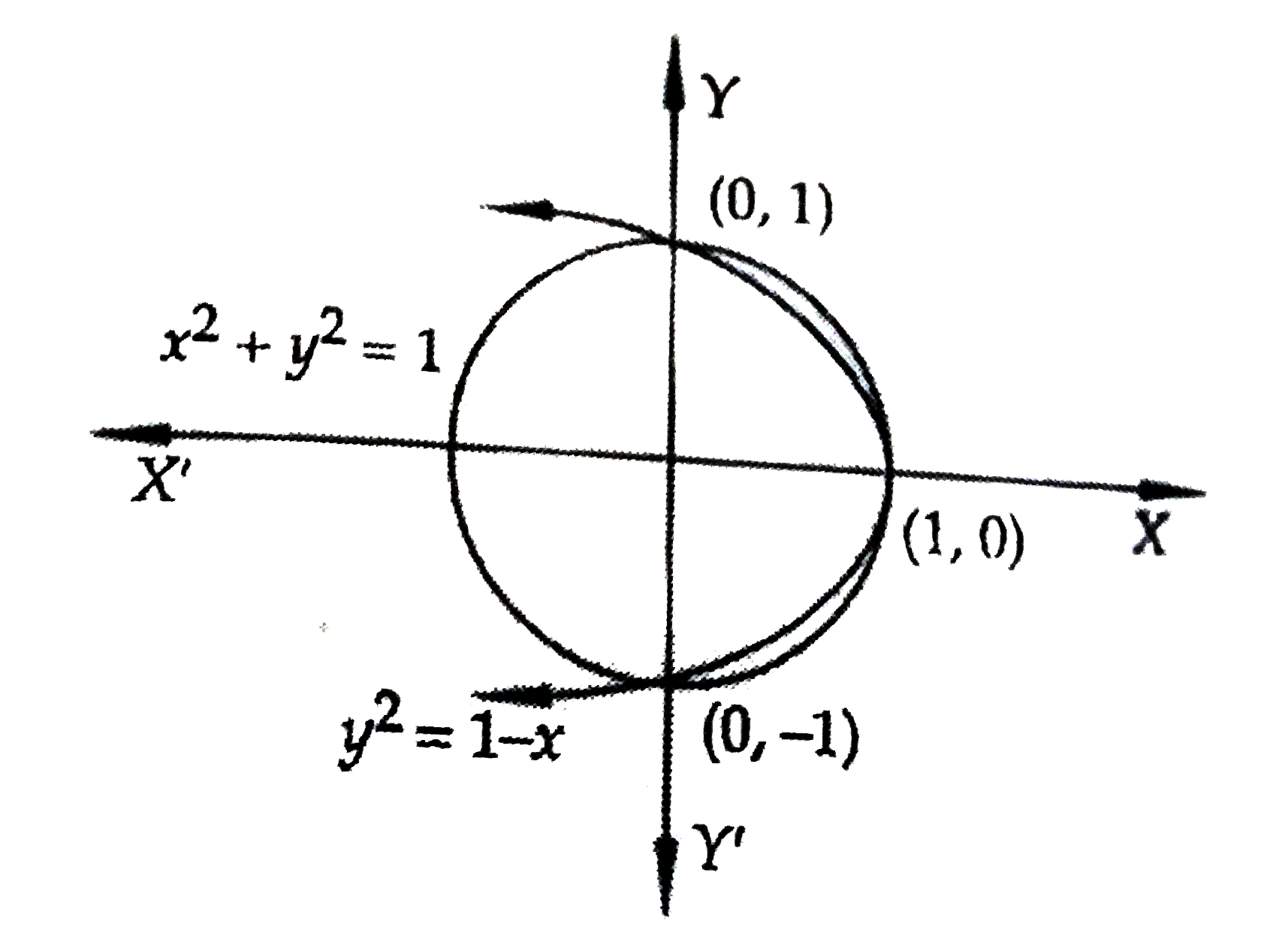
=π(1)2−21∫0(√1−x2−√1−x)dx
=π−2[12x√1−x2+12sin−1(x1)+23(1−x)3/2]10
π−2{π4−23}=π2+43
|
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
61 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
Similar Questions
The area of the region described by A={(x,y):x2+y2≤1andy2≤1−x} is
View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View SolutionThe area of the region {(x,y):x2+y2≤5,||x|−|y∣∣≥1 is
View SolutionThe area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
View SolutionFind the area of the region {(x,y):x2+y2≤1≤x+y}
View SolutionThe area of the region R={(x,y)/x2≤y≤x} is
View SolutionThe area of the region R={xy|x|≤|y∣andx2+y2≤1} is
View SolutionThe area of the region defined by ||x|−|y∣∣≤1andx2+y2≤1 in the xy plane is
View SolutionFind the area of the region given by x+y≤6,x2+y2≤6y and y2≤8x.
View SolutionThe area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
View Solution
