Let h(x)=f(x)−(f(x))2+(f(x))3 for every real number x. Then (a) h is increasing whenever f is increasing (b)h is increasing whenever f is decreasing (c)h is decreasing whenever f is decreasing (d) nothing can be said in general
h is increasing whenever is increasing
h is increasing whenever f is decreasing
h is decreasing whenever f is decreasing
nothing can be said in general
The correct Answer is:A, C
We have
Leth(x)=f(x)−{f(x)}2+{f(x)}3
h'(x)=f'(x)−2f(x)f'(x)+3{f(x)}2f'(x)
⇒h'(x)=f'(x)[1−2f(x)+3{f(x)2}]
⇒h'(x)=f'(x)(3y2−2y+1),wherey=f(x)
Consider the quadratic expression 3y2−2y+1 , Clearly discriminant of this quadratic expression is less than zero . So , its sign is always same as that of y2i.e.positive .
∴h'(x)=f'(x)×A positive real number
⇒Sign of h'(x) is same as that of f'(x)
⇒either h'(x)>0 and f'(x)>0orh'(x)<0andf'(x)<0
⇒ h(x) and f(x) increase and decrease together.
Topper's Solved these Questions
- INCREASING AND DECREASING FUNCTIONSBook:OBJECTIVE RD SHARMA ENGLISHChapter:INCREASING AND DECREASING FUNCTIONSExercise:Section II - Assertion Reason Type
Explore 8 Videos
- INCREASING AND DECREASING FUNCTIONSBook:OBJECTIVE RD SHARMA ENGLISHChapter:INCREASING AND DECREASING FUNCTIONSExercise:Exercise
Explore 36 Videos
- INCREASING AND DECREASING FUNCTIONSBook:OBJECTIVE RD SHARMA ENGLISHChapter:INCREASING AND DECREASING FUNCTIONSExercise:Chapter Test
Explore 18 Videos
- HEIGHTS AND DISTANCESBook:OBJECTIVE RD SHARMA ENGLISHChapter:HEIGHTS AND DISTANCESExercise:Exercise
Explore 45 Videos
- INDEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:INDEFINITE INTEGRALSExercise:Chapter Test
Explore 30 Videos
Similar Questions
Let g(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R. Then prove that g is increasing whenever is increasing.
View SolutionLet g(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R. Then prove that g is increasing whenever is increasing.
View SolutionLet h(x)=f(x)−a(f(x))3 for every real number x
h(x) increase as f(x) increses for all real values of x if
View SolutionThe function f(x)=x1+|x| is (a) strictly increasing (b) strictly decreasing (c) neither increasing nor decreasing (d) none of these
View SolutionThe function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
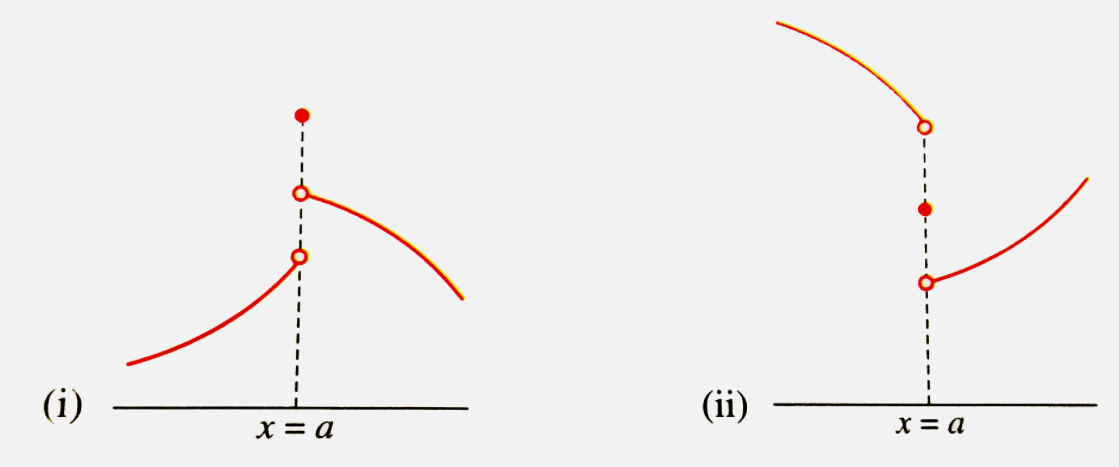
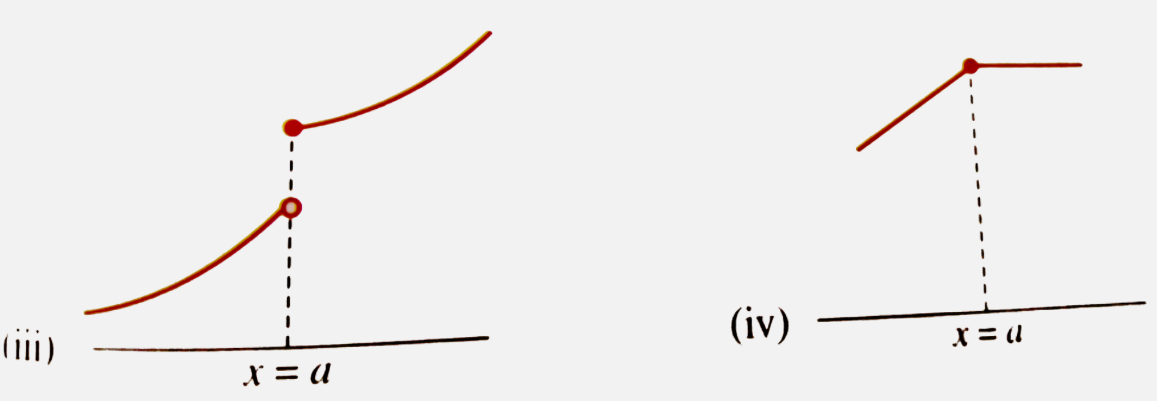
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing.
View SolutionWhich of the following statement is always true? (a)If f(x) is increasing, the f−1(x) is decreasing. (b)If f(x) is increasing, then 1f(x) is also increasing. (c)If fandg are positive functions and f is increasing and g is decreasing, then fg is a decreasing function. (d)If fandg are positive functions and f is decreasing and g is increasing, the fg is a decreasing function.
View SolutionState whether f(x)=tanx−x is increasing or decreasing its domain.
View Solution