Let f(x) be a function whose domain is [−5,7]. Let g(x)=|2x+5|, then domain of (fog)(x) is
A
[−5,1]
B
[−4,0]
C
[−6,1]
D
none of these
Video Solution
Text Solution
The correct Answer is:C
We have,
Domain(fog)={x:x∈Dom(g)andg(x)∈Dom(f)}
⇒Domain(fog)={x:x∈Rand|2x+5|∈[−5,7]}
⇒Domain(fog)={x:−5≤|2x+5|≤7}
⇒ Domain(fog)={x:0≤|2x+5|≤7}
⇒Domain(fog)={x:|2x+5|≤7}
⇒Domain(fog)={x:−7≤2x+5≤7}
⇒Domain(fog)={x:−12≤2x≤2}
⇒Domain(fog)={x:−6≤x≤1}=[−6,1]
|
Topper's Solved these Questions
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Section II - Assertion Reason Type
Explore 8 Videos
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Exercise
Explore 94 Videos
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Chapter Test
Explore 58 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBook:OBJECTIVE RD SHARMA ENGLISHChapter:PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMExercise:Chapter Test
Explore 55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS Book:OBJECTIVE RD SHARMA ENGLISHChapter:SCALAR AND VECTOR PRODUCTS OF THREE VECTORS Exercise:Exercise
Explore 63 Videos
Similar Questions
Knowledge Check
If f(x)=x−7andg(x)=√x, what is the domain of g∘f?
Ax≤0Bx≥−7Cx≥0Dx≥7
Find the domain of f(x)=5x−3
View SolutionLet f be a function whose domain is the set of all real number. If f(x)=|x|−x, what is the range of f?
View SolutionLet f be a function defined on [0,2]. Then find the domain of function g(x)=f(9x2−1)
View SolutionIf f(x)=√2−x and g(x)=√1−2x, then the domain of fog (x) is
View SolutionLet f(x)=x3+kx2+5x+4sin2x be an increasing function on x∈R. Then domain of k is
View SolutionConsider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
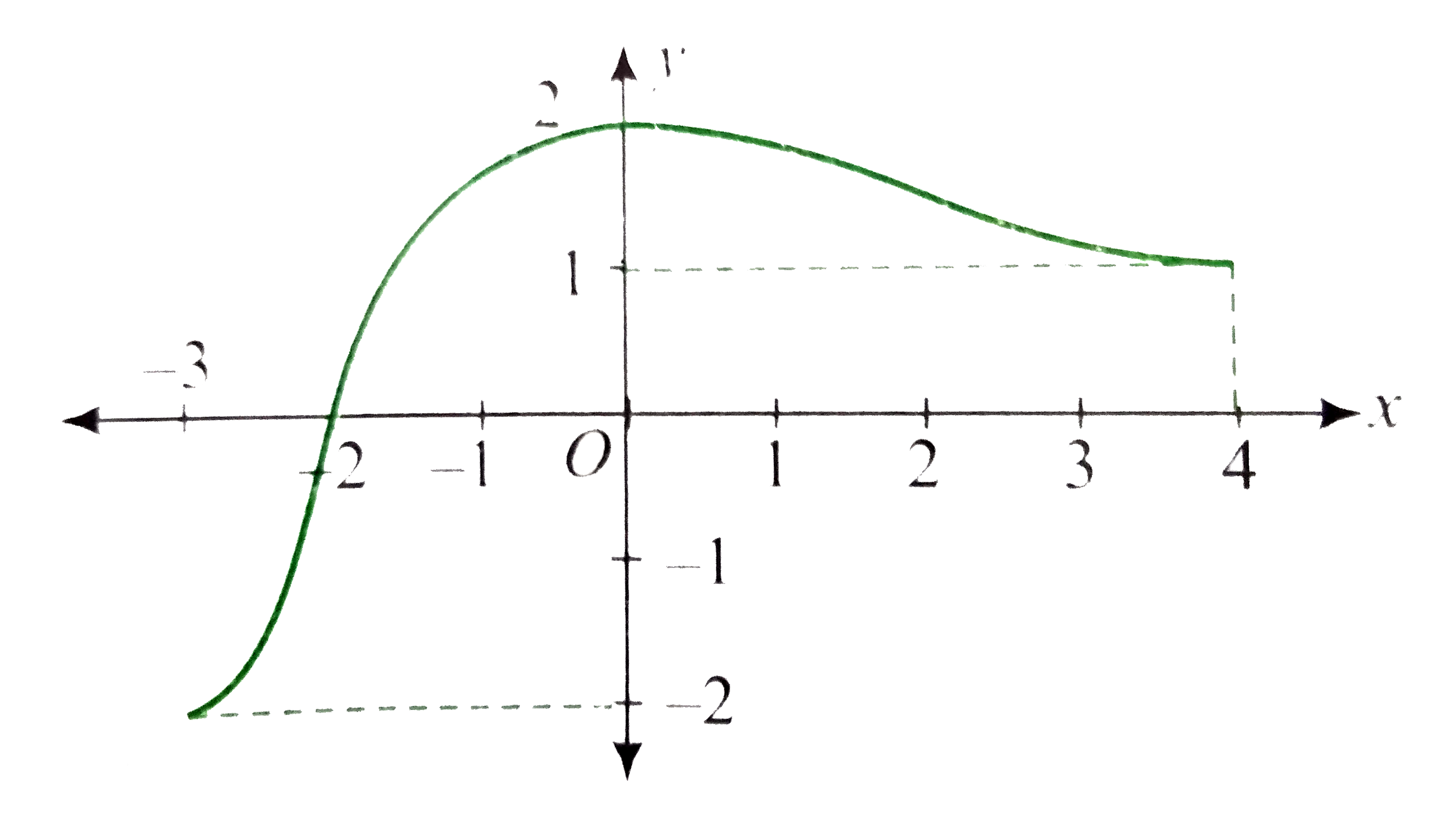
Domain and range of g(x)=f(|x|) is [a, b] and [c, d] respectively, then (b−a+c+d) is
View SolutionIf f(x) and g(x) are polynomial functions of x, then domain of f(x)g(x) is
View Solution