Let f(x)=logexandg(x)=x4−2x3+3x2−2x+22x2−2x+1
Then , the domain of fog (x) is
R
[0,∞)
(0,∞)
[1,∞)
The correct Answer is:A
To find the domain of the composite function f(g(x)), where f(x)=logex and g(x)=x4−2x3+3x2−2x+22x2−2x+1, we need to ensure that g(x)>0 since the logarithm function is only defined for positive values.
Step 1: Analyze the denominator of g(x)
The denominator of g(x) is 2x2−2x+1. We need to check if this expression is always positive.
1. Calculate the discriminant D of the quadratic:
D=b2−4ac=(−2)2−4⋅2⋅1=4−8=−4
Since the discriminant is negative, the quadratic does not have real roots and is always positive (as the coefficient of x2 is positive).
Step 2: Analyze the numerator of g(x)
Next, we need to analyze the numerator x4−2x3+3x2−2x+2 to determine when it is greater than zero.
1. We can factor or analyze the numerator. We can check for roots using the Rational Root Theorem or synthetic division, but a more straightforward approach is to evaluate the expression at various points.
2. Evaluate g(x) at specific points:
- At x=0:
g(0)=04−2⋅03+3⋅02−2⋅0+22⋅02−2⋅0+1=21=2>0
- At x=1:
g(1)=14−2⋅13+3⋅12−2⋅1+22⋅12−2⋅1+1=1−2+3−2+22−2+1=21=2>0
- At x=2:
g(2)=24−2⋅23+3⋅22−2⋅2+22⋅22−2⋅2+1=16−16+12−4+28−4+1=105=2>0
3. Since g(x) is a polynomial of degree 4, and we have evaluated it at several points and found it to be positive, we can conclude that g(x)>0 for all x.
Conclusion
Since g(x)>0 for all x, the domain of f(g(x)) is all real numbers.
Thus, the domain of f(g(x)) is:
Domain of f(g(x))=(−∞,∞)
D=b2−4ac=(−2)2−4⋅2⋅1=4−8=−4
Since the discriminant is negative, the quadratic does not have real roots and is always positive (as the coefficient of x2 is positive).
- At x=0:
g(0)=04−2⋅03+3⋅02−2⋅0+22⋅02−2⋅0+1=21=2>0
- At x=1:
g(1)=14−2⋅13+3⋅12−2⋅1+22⋅12−2⋅1+1=1−2+3−2+22−2+1=21=2>0
- At x=2:
g(2)=24−2⋅23+3⋅22−2⋅2+22⋅22−2⋅2+1=16−16+12−4+28−4+1=105=2>0
Domain of f(g(x))=(−∞,∞)
Topper's Solved these Questions
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type
8 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Exercise
94 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
63 Videos
Similar Questions
Knowledge Check
The graph of f(x)=x−3x2−2x−3 is shown below. What is the domain of f(x) ?
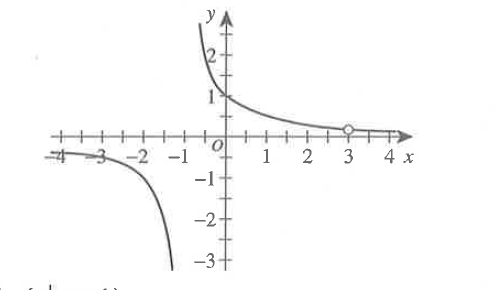 A{x∣x≠−1}B{x∣x≠2}C{x∣x≠3}D{x∣x≠−1andx≠3}
A{x∣x≠−1}B{x∣x≠2}C{x∣x≠3}D{x∣x≠−1andx≠3}
The domain of f(x)=log2(2x3−x2−4x+2), is
View SolutionFind fog if f(x)=x−2 and g(x)=3x
View SolutionLet f(x)=2x−sinx and g(x)=3√x . Then
View SolutionIf f:R→R,f(x)=x2+2x−3 and g:R→R,g(x)=3x−4 then the value of fog (x) is
View SolutionIf domain of f(x) is [1, 3], then the domain of f(log2(x2+3x−2)) is
View SolutionIf g(x)=2x2+3x−4 and g(f(x))=8x2+14x+1 then f (2) =
View SolutionThe domain of f(x) = x2x2−3x+2 is :
View Solution
