In the following figure, if the coordinates of P are (a,b,c) then the coordinates of A,B and C are respectively
(a,0,0),(b,0,0),(c,0,0)
(a,0,0),(0,b,0),(0,0,c)
(0,0,a),(0,b,0),(c,0,0)
(a,b,c),(b,c,a),(c,a,b)
The correct Answer is:A
To find the coordinates of points A, B, and C given that point P has coordinates (a, b, c), we can analyze the positions of these points in relation to the axes in a three-dimensional coordinate system.
1. Identify the coordinates of point A:
- Point A lies on the x-axis.
- By definition, any point on the x-axis has a y-coordinate and a z-coordinate of zero.
- Therefore, the coordinates of point A can be expressed as:
A=(a,0,0)
2. Identify the coordinates of point B:
- Point B lies on the y-axis.
- Similarly, any point on the y-axis has an x-coordinate and a z-coordinate of zero.
- Thus, the coordinates of point B are:
B=(0,b,0)
3. Identify the coordinates of point C:
- Point C lies on the z-axis.
- Any point on the z-axis has an x-coordinate and a y-coordinate of zero.
- Therefore, the coordinates of point C are:
C=(0,0,c)
Final Coordinates:
- The coordinates of A, B, and C are:
- A=(a,0,0)
- B=(0,b,0)
- C=(0,0,c)
- Point A lies on the x-axis.
- By definition, any point on the x-axis has a y-coordinate and a z-coordinate of zero.
- Therefore, the coordinates of point A can be expressed as:
A=(a,0,0)
- Point B lies on the y-axis.
- Similarly, any point on the y-axis has an x-coordinate and a z-coordinate of zero.
- Thus, the coordinates of point B are:
B=(0,b,0)
- Point C lies on the z-axis.
- Any point on the z-axis has an x-coordinate and a y-coordinate of zero.
- Therefore, the coordinates of point C are:
C=(0,0,c)
- The coordinates of A, B, and C are:
- A=(a,0,0)
- B=(0,b,0)
- C=(0,0,c)
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Section I - Solved Mcqs
16 Videos
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Exercise
20 Videos
- TANGENTS AND NORMALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - TANGENTS AND NORMALSEXERCISE - Chapter Test
25 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Chapter Test
60 Videos
Similar Questions
In the adoining figure if the coordinates of point P are (a,b,c) write the coordinates of A,B,C,D,E and F.
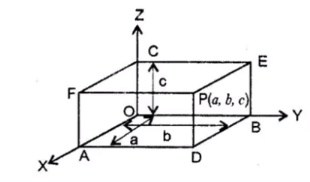
View SolutionIn following figure, coordinates of P are

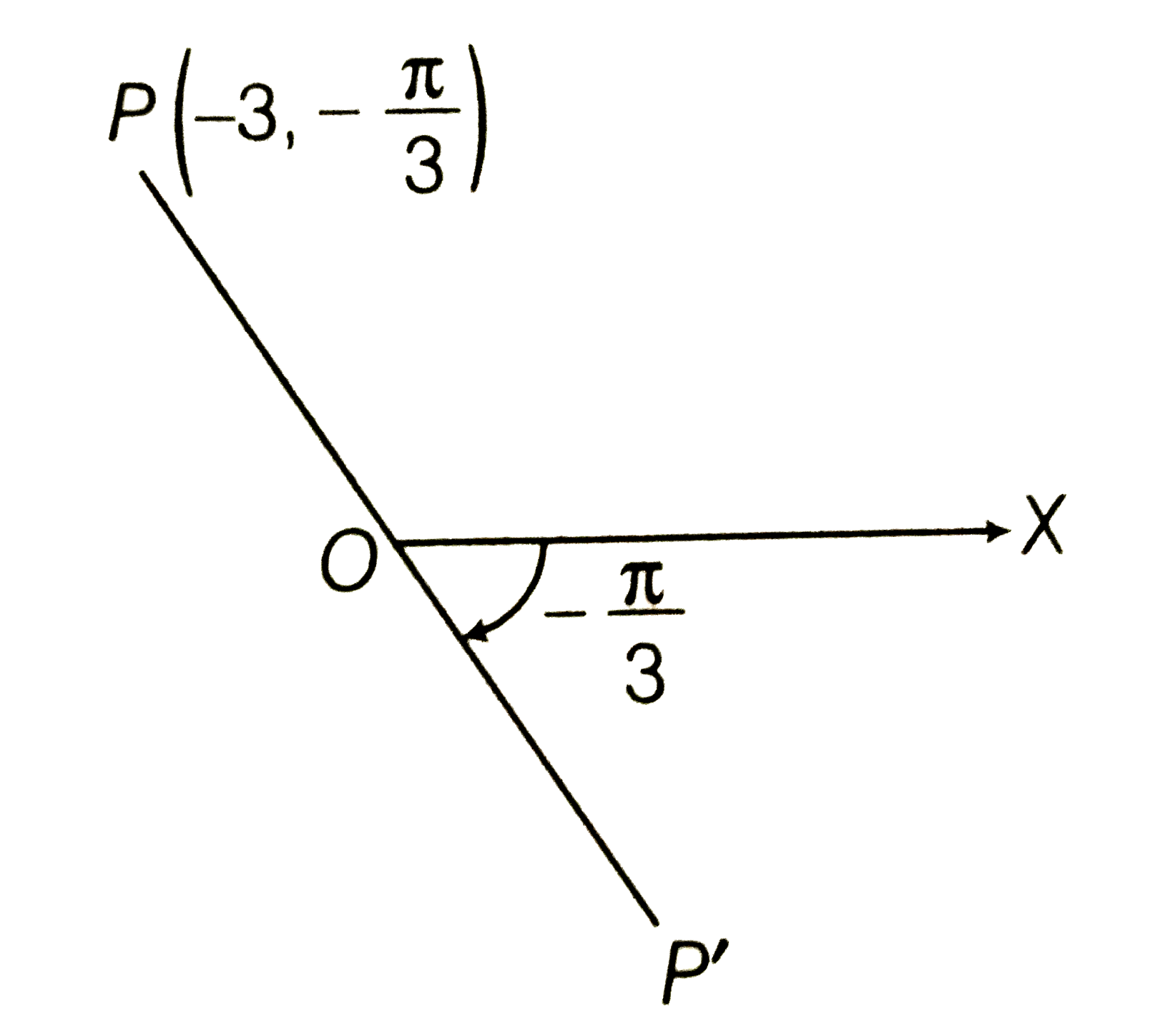
View SolutionThe coordinates of P' in the figure is
View SolutionSee Fig. 3.11 and complete the following statements:(i) The abscissa and the ordinate of the point B are _and _ Hence, the coordinates of B are (__,__).(ii) The x–coordinate and the y–coordinate of the point M are _ and _ respectively. Hence, the coordinates of M are (__,__).(iii) The x–coordinate and the y–coordinate of the point L are _ and _ respectively. Hence, the coordinates of L are (__,__).(iv) The .r–coordinate and the y–coordinate of the point S are _ and _ respectively. Hence, the coordinates of S are (__,__).
View SolutionFor a solid with the structure shown in Fig, the coordination number of the points of the points A and B, respectively are

View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinates of the point C.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,5,7)and (1,7,6), respectively, find the coordinates of the point C.
View Solutionx coordinates of two points B and C are the roots of equation x2+4x+3=0 and their y coordinates are the roots of equation x2−x−6=0. If x coordinate of B is less than the x coordinate of C and y coordinate of B is greater than the y coordinate of C and coordinates of a third point A be (3,−5), find the length of the bisector of the interior angle at A.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1, 3) and C(-2, 7). The coordinates of vertex A can be
View Solution
