A vector →r is inclined at equal to OX,OYandOZ. If the magnitude of →r is 6 units, find →r.
Let l,m,n be the direction cosines of →r which is equally inclined to the coodinate axes. Then,
∴l=m=n=−1√3
Hence →r=|→r|(lˆi+mˆj+nˆk)
⇒→r=6(±1√3ˆi±1√3ˆj±1√3ˆk)⇒→r=2√3(±ˆi±ˆj±ˆk)
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Section I - Solved Mcqs
16 Videos
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Exercise
20 Videos
- TANGENTS AND NORMALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - TANGENTS AND NORMALSEXERCISE - Chapter Test
25 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Chapter Test
60 Videos
Similar Questions
Knowledge Check
If →a and →b are unit vectors inclined at an angle α, then the value of ∣∣→a−→b∣∣ is
A2sinα2B2cosα2C2sinαD2cosα
A vector →OP is inclined to OXat450andOYat600 . Find the angle at which →OP is inclined to OZ.
View SolutionA vector →r is inclined to x-axis at 450 and y-axis at 600. If |→r|=8 units, find →r.
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
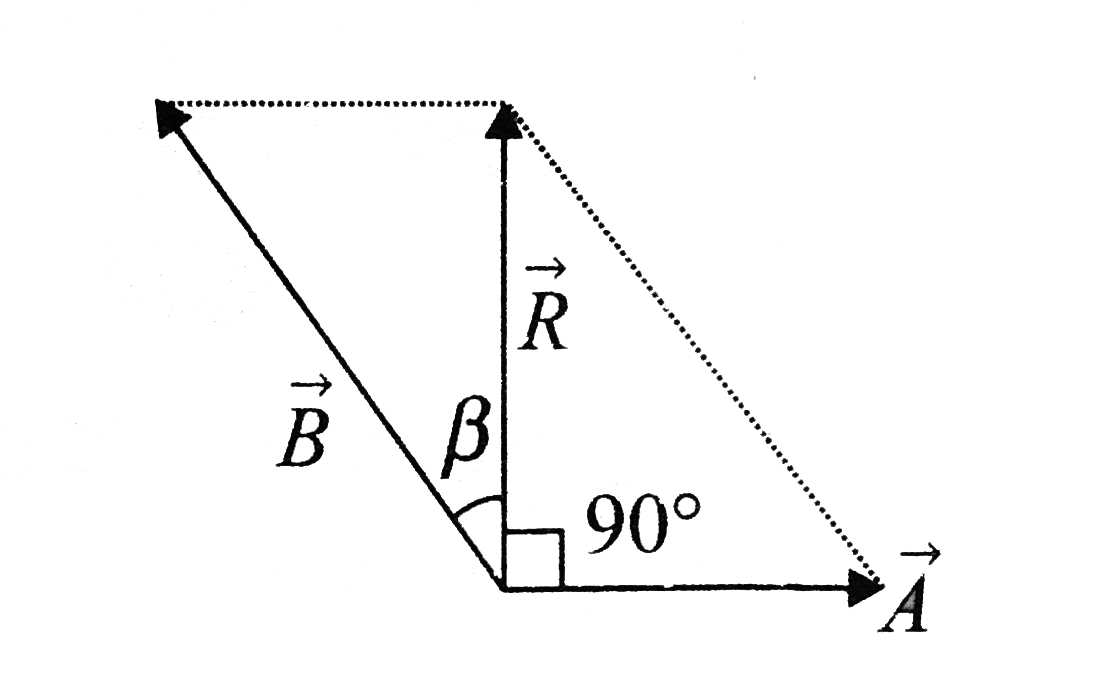
View SolutionIf →a and →b are two vectors such that (→a+→b).→a−→b=0 find the relation between the magnitudes of →a and →b.
View SolutionLet →a⋅→b=0,where→aand→b are unit vectors and the unit vector →c is inclined at an angle θ to both →aand→b. If →c=m→a+n→b+p(→a×→b),(m,n,p∈R), then a.−π4≤θ≤π4 b. π4≤θ≤3π4 c. 0≤θ≤π4 d. 0≤θ≤3π4
View SolutionShow that the vector i+j+k is equally inclined with the axes OX, OY and OZ.
View SolutionIf →r is a vector of magnitude 21 and has direction ratios 2,−3and6, then find →r.
View Solution
