Question

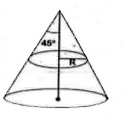
The semi-vertical angle of a cone is ${45}^{\circ }$ . If the height of the cone is 20.025, then its approximate laternal surface area, is

Options

A. `401sqrt(2) pi`
B. `400sqrt(2) pi`
C. `399sqrt(2) pi`
D. none of these

Answer

A

Explanation

To find the approximate lateral surface area of a cone with a semi-vertical angle of $${45}^{\circ }$$ and a height of $$20.025$$, we can follow these steps:

Step 1: Understand the Geometry of the Cone
Given that the semi-vertical angle is \(45^\circ\), we can deduce that the radius \(R\) of the cone is equal to its height \(H\). This is because in a right triangle formed by the radius, height, and slant height, if the angle is \(45^\circ\), then:

\( H = R \)

Step 2: Use the Pythagorean Theorem
The slant height \(L\) can be calculated using the Pythagorean theorem:

\( L^2 = H^2 + R^2 \)

Since \(H = R\), we can substitute \(R\) with \(H\):

\( L^2 = H^2 + H^2 = 2H^2 \)

Thus,

\( L = H\sqrt{2} \)

Step 3: Define the Lateral Surface Area Formula
The formula for the lateral surface area \(S\) of a cone is given by:

\( S = \pi R L \)

Substituting \(R\) and \(L\) in terms of \(H\):

\( S = \pi H (H\sqrt{2}) = \pi H^2 \sqrt{2} \)

Step 4: Substitute the Height
Given that the height \(H\) is \(20.025\), we can express \(S\) as:

\( S = \pi (20.025)^2 \sqrt{2} \)

Step 5: Calculate \(S\)
First, calculate \(20.025^2\):

\( 20.025^2 = 400.100625 \)

Now substitute this value into the equation for \(S\):

\( S = \pi \cdot 400.100625 \cdot \sqrt{2} \)

Step 6: Approximate the Change in Height
To find the approximate change in lateral surface area due to a small change in height, we denote the change in height as \(\Delta H = 0.025\). We need to find the derivative of \(S\) with respect to \(H\):

\( \frac{dS}{dH} = 2\pi H \sqrt{2} \)

Now evaluate this at \(H = 20\):

\( \frac{dS}{dH} \bigg|_{H=20} = 2\pi (20) \sqrt{2} = 40\pi \sqrt{2} \)

Step 7: Calculate the Change in Surface Area
The change in surface area \(\Delta S\) can be calculated as:

\( \Delta S = \frac{dS}{dH} \cdot \Delta H = 40\pi \sqrt{2} \cdot 0.025 = \pi \sqrt{2} \cdot 1 \)

Step 8: Final Approximate Lateral Surface Area
Now, we can find the approximate lateral surface area:

\( S_{\text{approx}} = S + \Delta S \)

Substituting the values we have:

\( S_{\text{approx}} = \pi \cdot 400 \sqrt{2} + \pi \sqrt{2} = \pi \sqrt{2} (400 + 1) = 401\pi \sqrt{2} \)

Conclusion
Thus, the approximate lateral surface area of the cone is:

\( \boxed{401\pi\sqrt{2}} \)