A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is .
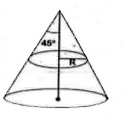
What will be the tension in the ring?
The correct Answer is:B
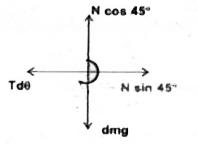
FBD of small section of ring subtending angle at centre of ring is as shown.
Similar Questions
For a uniform ring of mass M and radius R at its centre
View SolutionA chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View SolutionA ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−

View SolutionConsider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionA metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
View Solution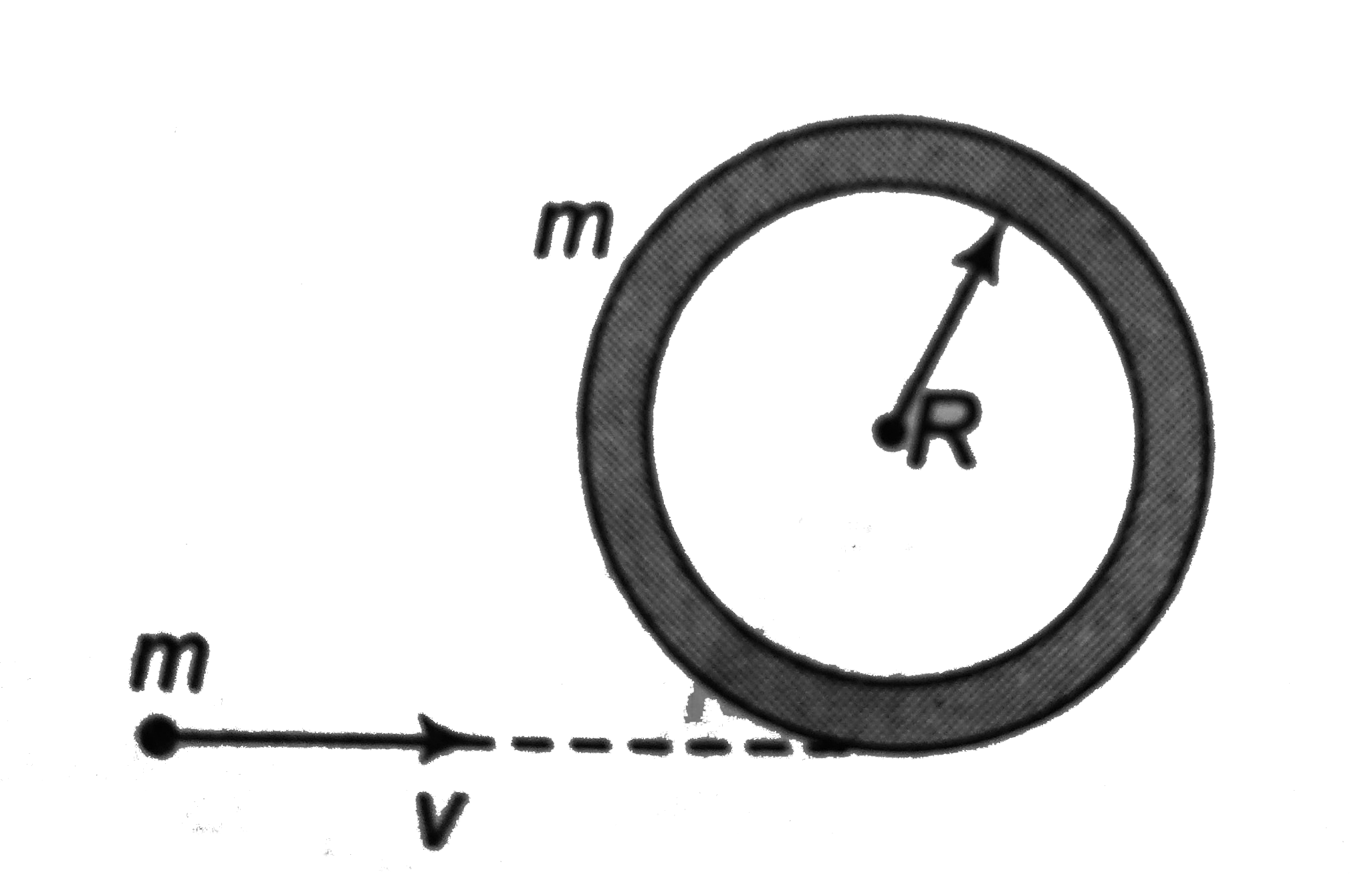
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionA solid sphere of radius r is melted and cast into the shape of a solid cone of height r , the radius of the base of the cone is
View Solution
