The equations of the circle which touches the axis of y at the origin and passes through (3, 4) , is

A

$2 (x^{2} + y^{2}) - 3 x = 0$

B

$3 (x^{2} + y^{2}) - 25 x = 0$

C

$4 (x^{2} + y^{2}) - 25 x = 0$

D

$4 (x^{2} + y^{2}) - 25 x + 10 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The centre of the circle lies on x-axis. Let a be the radius of the circle. Then, coordinates of the centre are (a, 0).
The circle passes through (3, 4). Therefore,
$\sqrt{{(a - 3)}^{2} + {(0 - 4)}^{2}} = a \Rightarrow - 6 a + 25 = 0 \Rightarrow a = \frac{25}{6}$
So, the equation of the circle is ${(x - a)}^{2} + {(y - 0)}^{2} = a^{2}$
$\Rightarrow x^{2} + y^{2} - 2 a x = 0 \Rightarrow 3 (x^{2} + y^{2}) - 25 x = 0$
(V) when the circle touches both the axes
In this case, we have h =k = a
Hence, the equation of the circle is
${(x - a)}^{2} + {(y - a)}^{2} = a^{2}$ or, $x^{2} + y^{2} - 2 a x - 2 a y + a^{2} = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

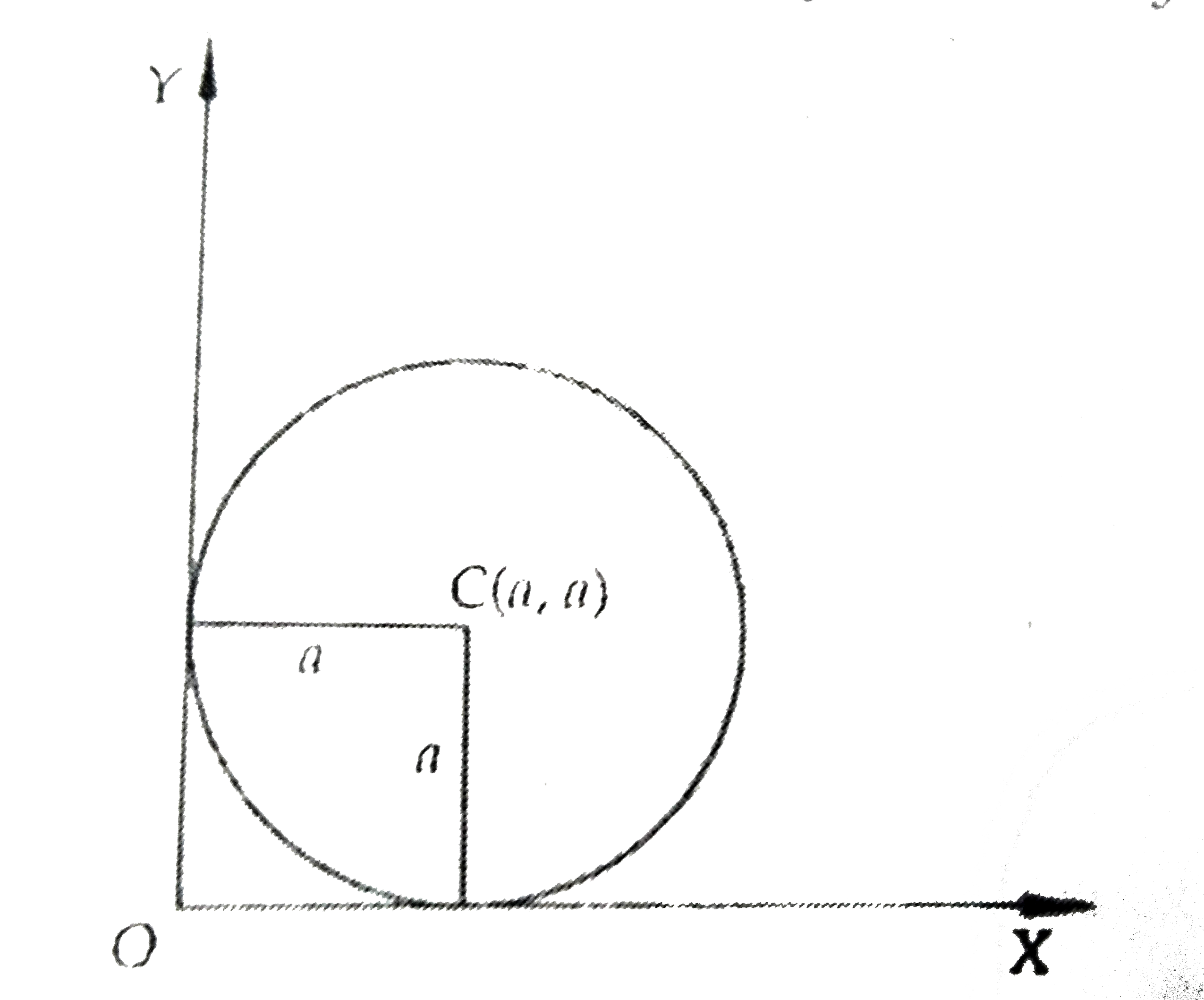
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of a circle which touches the y-axis at origin and whose radius is 3 units is
A $x^{2} + y^{2} \pm 6 y = 0$
B $x^{2} + y^{2} \pm 6 x = 0$
C $x^{2} + y^{2} \pm 3 x = 0$
D $x^{2} + y^{2} \pm 3 y = 0$

OBJECTIVE RD SHARMA ENGLISH-CIRCLES-Chapter Test

Home
Ask Doubt
Profile