If the line 4x−3y=−12 is tangent at point (−3,0) and the line 3x+4y=16 is tangent at the point (4,1) to a circle then equation of circle
x2+y2−2x+6y−15=0
x2+y2−2x+6y−20=0
x2+y2+2x+6y−15=0
x2+y2−2x−6y−15=0
The correct Answer is:A
Clearly, centre C of the required circle is the point of intersection of the normals at A and B.
The equation of a line through A (-3, 0) and perpendicular to 4x-3y=-12 is
y−0=−34(x+3)⇒3x+4y+9=0 ...(i)
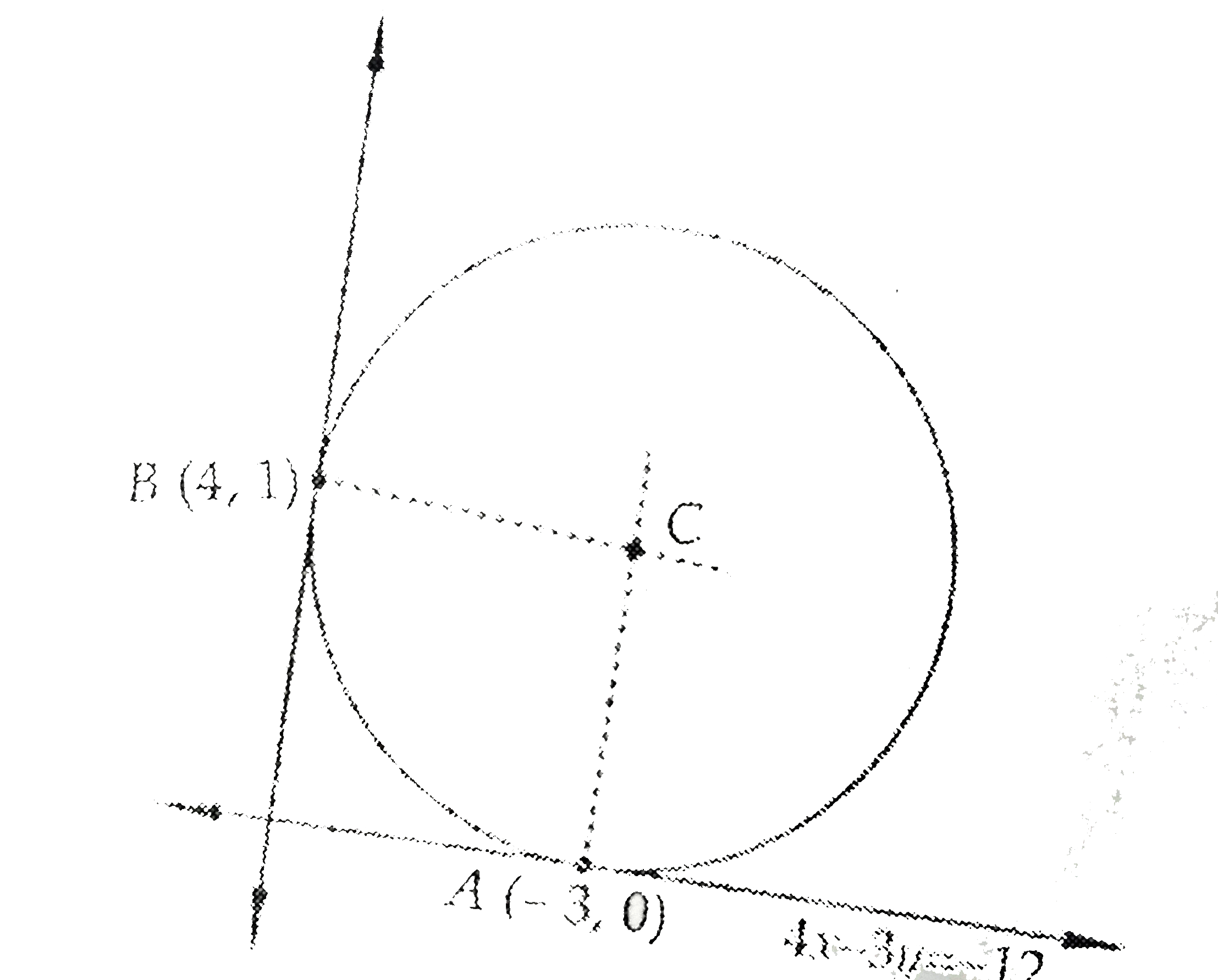
Similarly, the equation of a line through B(4, 1) and perpendicular to 3x+4y=16 is
y−1=43(x−4)⇒4x−3y−13=0 ...(ii)
Solving (i) and (ii), we get x=1, y=-3.
So, the coordinates of C are (1, -3).
∴ Radius =CA=√16+9=5.
Hence, the equation of the required circle is
(x−1)2+(y+3)2=52 or, x2+y2−2x+6y−15=0
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
Centre of a circle of radius 4√5 lies on the line y=x and satisfies the inequality 3x+6y>10. If the line x+2y=3 is a tangent to the circle, then the equation of the circle is
View SolutionThe line 5x−y=3 is a tangent to a circle at the point (2,7) and its centre is on theline x+2y=19. Find the equation of the circle.
View Solution
Knowledge Check
If the lines 3 x - 4y + 4 = 0 and 6x - 8y - 7 = 0 are tangents to a circle , then the radius of the circle is
A34 unitsB32 unitsC3 unitsD23 units
If the line x+3y=0 is tangent at (0,0) to the circle of radius 1, then the centre of one such circle is
View SolutionShow that the line x−y+4=0 is tangent to the parabola y2=16x. Find the point of contact.
View SolutionIf the lines 3x−4y+4=0 and 6x−8y−7=0 are tangents to a circle, then find the radius of the circle.
View SolutionIf the lines 3x−4y+4=0 and 6x−8y−7=0 are tangents to a circle, then find the radius of the circle.
View SolutionIf the lines 3x−4y+4=0 and 6x−8y−7=0 are tangents to a circle, then find the radius of the circle.
View SolutionIf the lines 3x−4y+4=0 and 6x−8y−7=0 are tangents to a circle, then find the radius of the circle.
View SolutionThe line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View Solution
