Angle at which the circle x2+y2=16 can be seen from (8,0) is
30∘
60∘
150∘
120∘
The correct Answer is:B
Here, we have to find the angle between the tangents drawn from point P(8, 0) to the circle x2+y2=16.
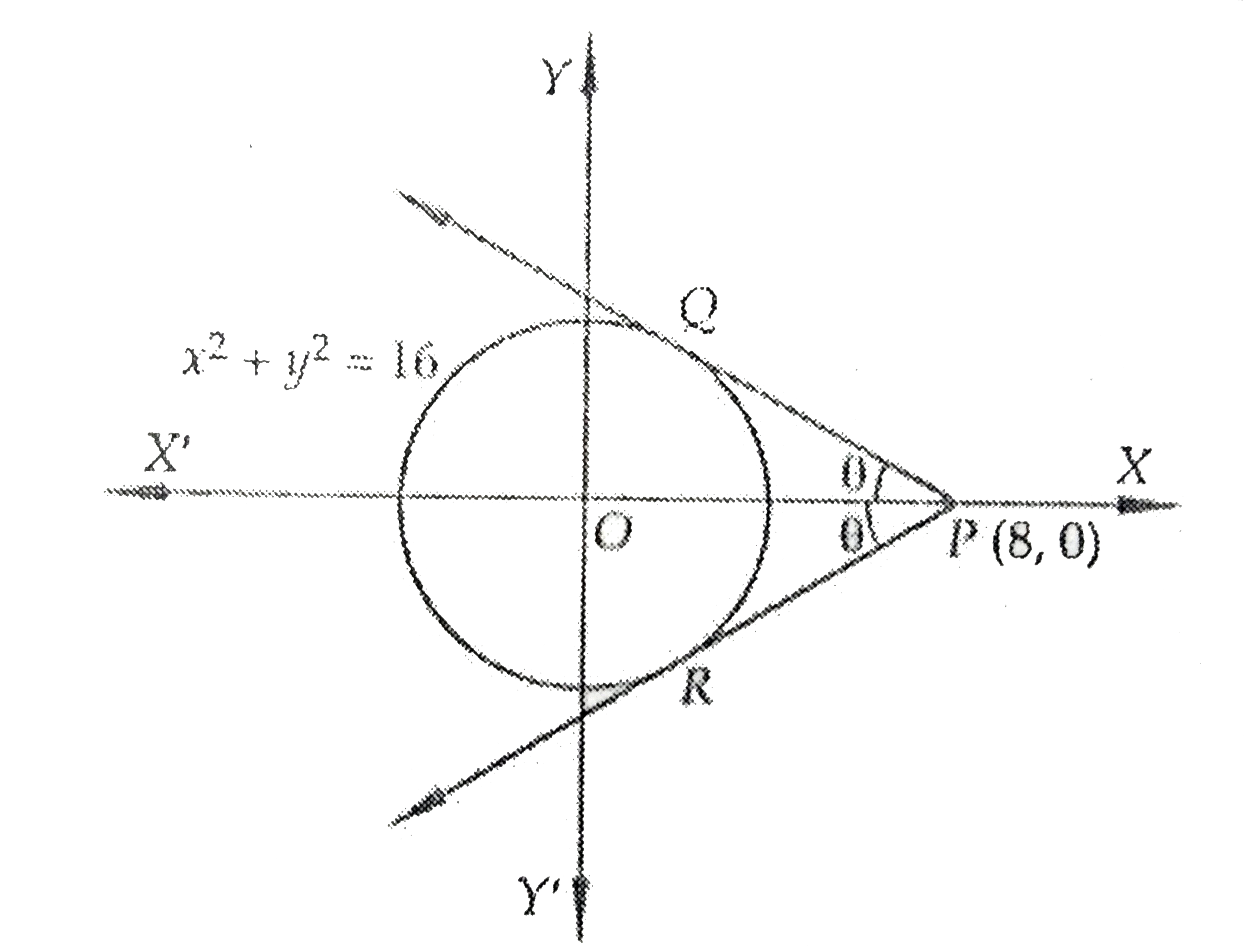
The equation of any line through (8, 0) is
y=m(x-8) or, mx-y-8m=0
If it touches the circle x2+y2=16, then
∣∣∣−8m√m2+1∣∣∣=4⇒4m2=m2+1⇒m=±1√3
Thus, the two tangents make 30∘ and 150∘ angles with OX.
Therefore, required angle is of 60∘ Hence, the angle at which the circle x2+y2=16 can be seen from the point (8, 0) is of 60∘.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
Find the angle at which the circles x2+y2+x+y=0 and x2+y2+x−y=0 intersect.
View SolutionThe number of common tangents of the circles x2+y2=16 and x2+y2−2y=0 is :
View SolutionA point on the line x=3 from which the tangents drawn to the circle x2+y2=8 are at right angles is
View SolutionTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
View SolutionThe point on the straight line y=2x+11 which is nearest to the circle 16(x2+y2)+32x−8y−50=0 is
View SolutionIf the tangent to the ellipse x2+4y2=16 at the point 0 sanormal to the circle x2+y2−8x−4y=0 then θ is equal to
View SolutionEquation of the circle concentric with the circle
x2+y2+8x+10y−7=0 , and passing through the centre of the circle x2+y2−4x−6y=0,is
View SolutionThe locus of the point of intersection of the tangent to the circle x2+y2=a2 ,which include an angle of 45 is the curve (x2+y2)2=λ(a2)(x2+y2−a2). the value of lambda(λ) is : (a) 2 (b) 4 (c)8 (d) 16
View SolutionFind the equation of the image of the circle x2+y2+8x−16y+64=0 in the line mirror x=0.
View SolutionFind the equations of the common tangents to the circle x2+y2=8 and the parabola y2=16x.
View Solution
