The angle between a pair of tangents from a point P to the circe x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. Find the equation of the locus of the point P.
x2+y2+4x−6y+4=0
x2+y2+4x−6y−9=0
x2+y2+4x−6y−4=0
x2+y2+4x−6y+9=0
The correct Answer is:D
The coordinates of the centre and radius of the given circle are (-2, 3) and √4+9−9sin2α−13cos2α=2sinα respectively .
Let the coordinates of CP be (h, k).
Clearly, CP bisects ∠TPT'=2α
∴∠CPT=∠CPT'=α
Now, in ΔCPT, we have
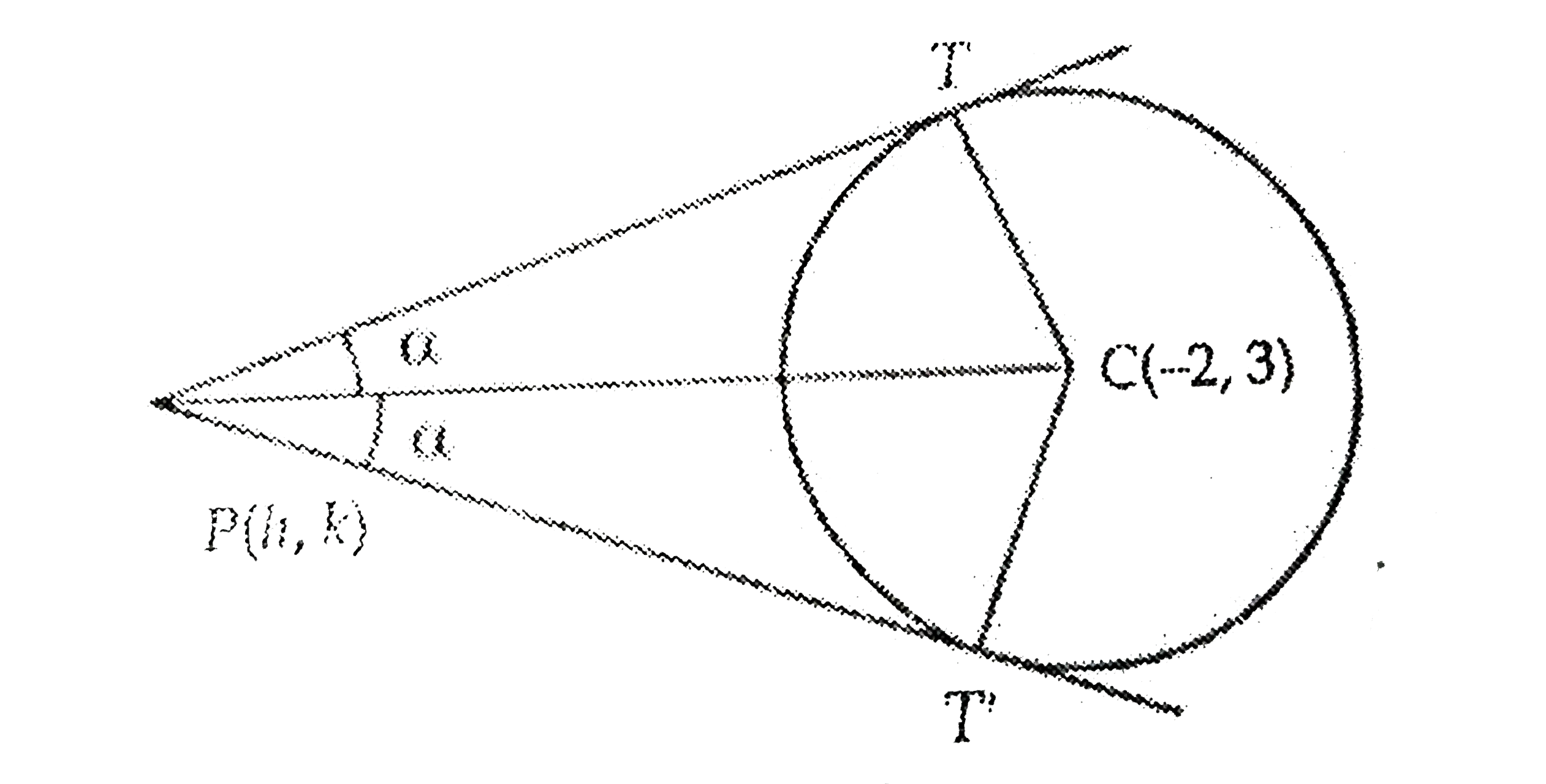
sinα=CTCP
⇒sinα=2sinα√(h+2)2+(k−3)2
⇒(h+2)2+(k−3)2=4⇒h2+k2+4h−6k+9=0
Hence, the locus of (h, k) is x2+y2+4x−6y+9=0
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs108videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test30videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
Similar Questions
The angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is a. x2+y2+4x−6y+4=0 b. x2+y2+4x−6y−9=0 c. x2+y2+4x−6y−4=0 d, x2+y2+4x−6y+9=0
View SolutionThe angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is x2+y2+4x−6y+4=0 x2+y2+4x−6y−9=0 x2+y2+4x−6y−4=0 x2+y2+4x−6y+9=0
View SolutionThe angle between a pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α. The equation of the locus of the point P is
View SolutionThe angle between the pair of tangents from the point (1,12) to the circle x2+y2+4x+2y−4=0 is
View SolutionThe angle between a pair of tangents from a point P to the circle x2+y2−6x−8y+9=0 is π3. Find the equation of the locus of the point P.
View SolutionThe angle between a pair of tangents drawn from a point P to the hyperbola y2=4ax is 45∘. Show that the locus of the point P is hyperbola.
View SolutionFind the equations of the tangents from the point A(3,2) to the circle x2+y2+4x+6y+8=0.
View SolutionIf a point P is moving such that the lengths
of the tangents drawn form P to the circles
x2+y2+8x+12y+15=0and
x2+y2−4x−6y−12=0 are equal
then find the equation of the locus of PView SolutionIf a point P is moving such that the lengths of tangents drawn from P to the circles
x2+y2−4x−6y−12=0 and
x2+y2+6x+18y+26=0 are the ratio 2:3, then find the equation to the locus of P.View SolutionFind the condition that the chord of contact of tangents from the point (α,β) to the circle x2+y2=a2 should subtend a right angle at the centre. Hence find the locus of (α,β).
View Solution

