Prove that the angle between the tangents from (α,β) to the circle x2+y2=a2 is 2tan−1(a√S1) , where S1=α2+β2−a2
tan−1(a√S1)
2tan−1(a√S1)
2tan−1(√S1a)
none of these
The correct Answer is:B
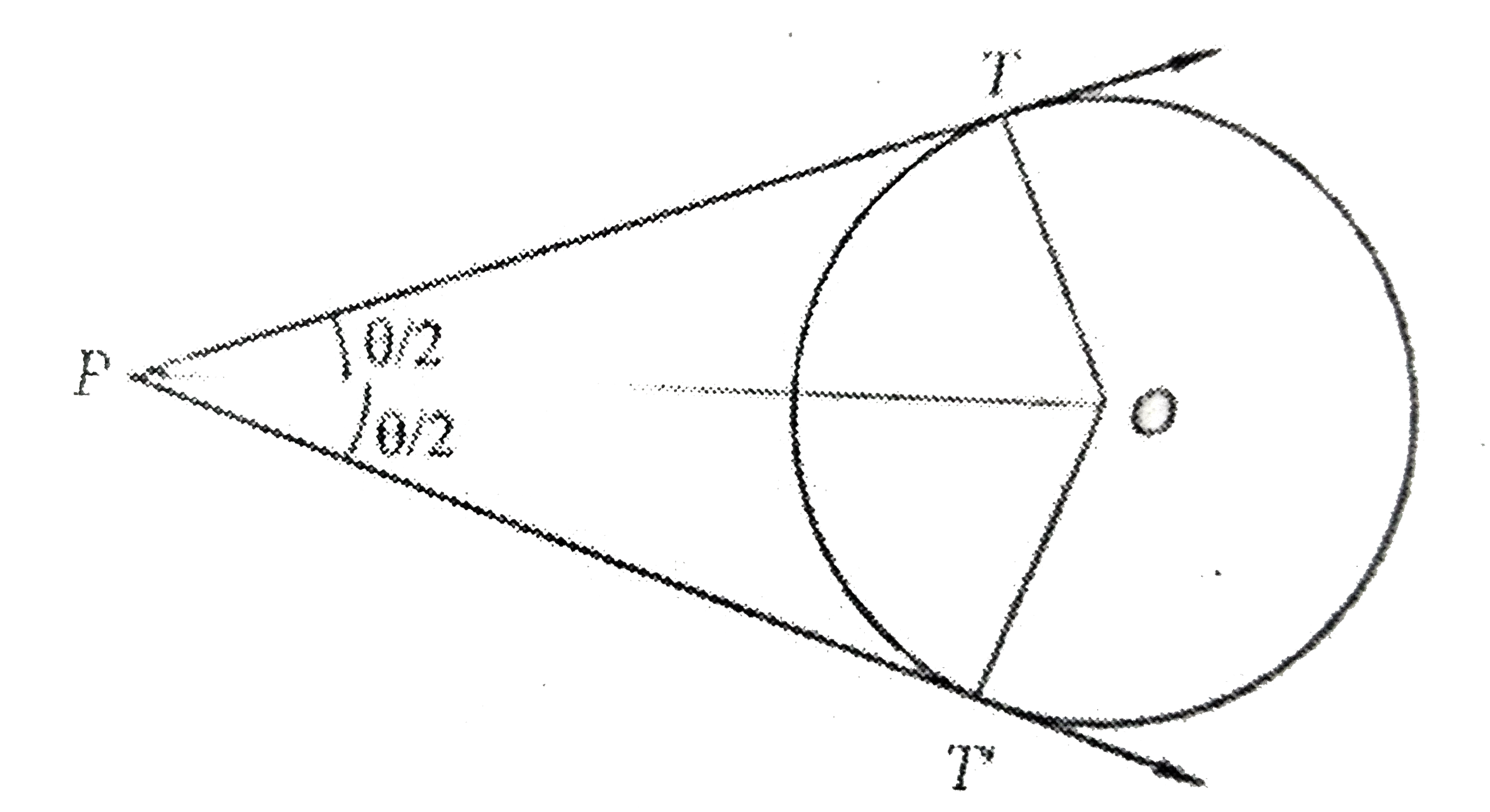
Let PT and PT' be the tangents drawn from P(α,β) to the circle x2+y2=a2, and let ∠TPT'=θ. If O is the centre of the circle, then
∠TPO=∠T'PO=θ/2
∴tan.θ2=OTOP=a√S1⇒θ=2tan−1(a√S1
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
If S1=α2+β2−a2, then angle between the tangents from (α,β) to the circle x2+y2=a2, is
View SolutionIf the chord of contact of the tangents from the point (α,β) to the circle x2+y2=r21 is a tangent to the circle (x−a)2+(y−b)2=r22, then
View SolutionFind the condition that the chord of contact of tangents from the point (α,β) to the circle x2+y2=a2 should subtend a right angle at the centre. Hence find the locus of (α,β).
View SolutionFind the condition that the chord of contact of tangents from the point (α,β) to the circle x2+y2=a2 should subtend a right angle at the centre. Hence find the locus of (α,β).
View SolutionI If a point (α,β) lies on the circle x2+y2=1 then the locus of the point (3α.+2,β), is
View Solution(1+tanαtanβ)2+(tanα−tanβ)2=
View SolutionProve that: tan(α+β)tan(α−β)=sin2α−sin2βcos2α−sin2β
View SolutionIf tanβ=3tanα, prove that tan(α+β)=2sin2β1+cos2β
View SolutionIf tangent of y2=x at (α,β), where β>0 is also a tangent of ellipse x12y2=1 then value of α is
View Solutionαandβ are acute angles and cos2α=3cos2β−13−cos2β then tanαcotβ=
View Solution
