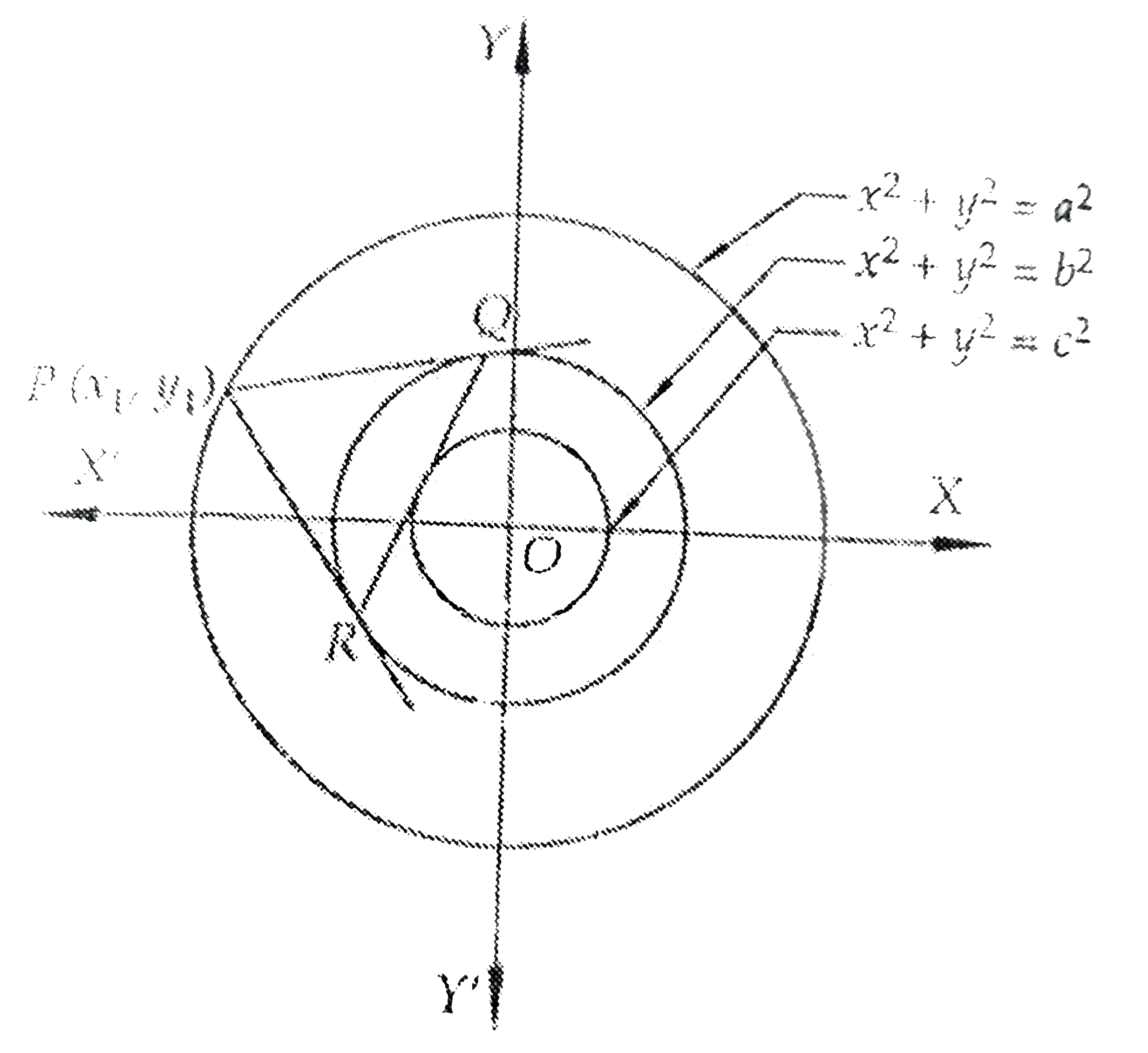
If the chord of contact of the tangents drawn from a point on the circle x2+y2=a2 to the circle x2+y2=b2 touches the circle x2+y2=c2 , then prove that a,b and c are in GP.
A.P.
G.P.
H.P.
none of these
The correct Answer is:B
Let P(x1,y1) be a point on the circle x2+y2=a2
Then,
x21+y21=a2 ...(i)
The equation of the chord of contact of tangents drawn from (x1,y1) to the circle x2+y2=b2 is
xx1+yy1=b2 ...(ii)
This touches the circle x2+y2=c2
∴ Length of the perpendicular from (0, 0) to line (ii) is equal to the radius of x2+y2=c2
⇒∣∣
∣
∣∣0×x1+0×y1−b2√x21+y21∣∣
∣
∣∣=c
⇒b2√a2=c [Using (i)]
⇒b2=ac⇒a,b,c are in G.P.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
If the chord of contact of the tangents from a point on the circle x2+y2=a2 to the circle x2+y2=b2 touch the circle x2+y2=c2, then the roots of the equation ax2+2bx+c=0 are necessarily. (A) imaginary (B) real and equal (C) real and unequal (D) rational
View SolutionIf the chord of contact of the tangents from a point on the circle x2+y2=a2 to the circle x2+y2=b2 touch the circle x2+y2=c2, then the roots of the equation ax2+2bx+c=0 are necessarily. (A) imaginary (B) real and equal (C) real and unequal (D) rational
View SolutionIf the chord of contact of tangents from a point (x1,y1) to the circle x2+y2=a2 touches the circle (x−a)2+y2=a2, then the locus of (x1,y1) is
View SolutionThe length of the chord of contact of the tangents drawn from the point (−2,3) to the circle x2+y2−4x−6y+12=0 is:
View SolutionIf the chord of contact of tangents from a point P(h, k) to the circle x2+y2=a2 touches the circle x2+(y−a)2=a2, then locus of P is
View Solution(prove that) If the polar of the points on the circle
x2+y2=a2 with respect to the circle
x2+y2=b2 touches the circle x2+y2=c2
then prove that a, b, c, are in Geometrical
progression.
View SolutionThe angle between the tangents drawn from a point on the director circle x2+y2=50 to the circle x2+y2=25, is
View SolutionThe chords of contact of the pair of tangents drawn from each point on the line 2x+y=4 to the circle x2+y2=1 pass through the point (h,k) then 4(h+k) is
View SolutionIf the chord of contact of the tangents drawn from the point (h,k) to the circle x2+y2=a2 subtends a right angle at the center, then prove that h2+k2=2a2.
View SolutionTangents drawn from a point on the circle x2+y2=9 to the hyperbola x225−y216=1,
then tangents are at angle
View Solution
