Question

Tangents are drawn from the point (h,k) to ^circle $x^2+y^2=a^2$; Prove that the area of the triangle formed by them and the straight line joining their point of contact is $\frac{a{(h^2+k^2-a^2)}^{\frac{3}{2}}}{h^2+k^2}$

Options

A. `((h^(2)+k^(2)-a^(2))^(3//2))/(h^(2)+k^(2))`
B. `(a(h^(2)+k^(2)-a^(2))^(1//2))/(h^(2)+k^(2))`
C. `(a(h^(2)+k^(2)-a^(2))^(1//2))/(h^(2)+k^(2))`
D. `((h^(2)+k^(2)-a^(2))^(3//2))/(a(h^(2)+k^(2)))`

Answer

B

Explanation

The equation of the circle is
`x^(2)+y^(2)=a^(2) " " ...(i)`
The equation of the chord of contact of tangents drawn from p(h, k) to the circle (i) is
`hx+ky-a^(2)=0 " " ...(ii)`
We have to find the area of `DeltaPQR`.

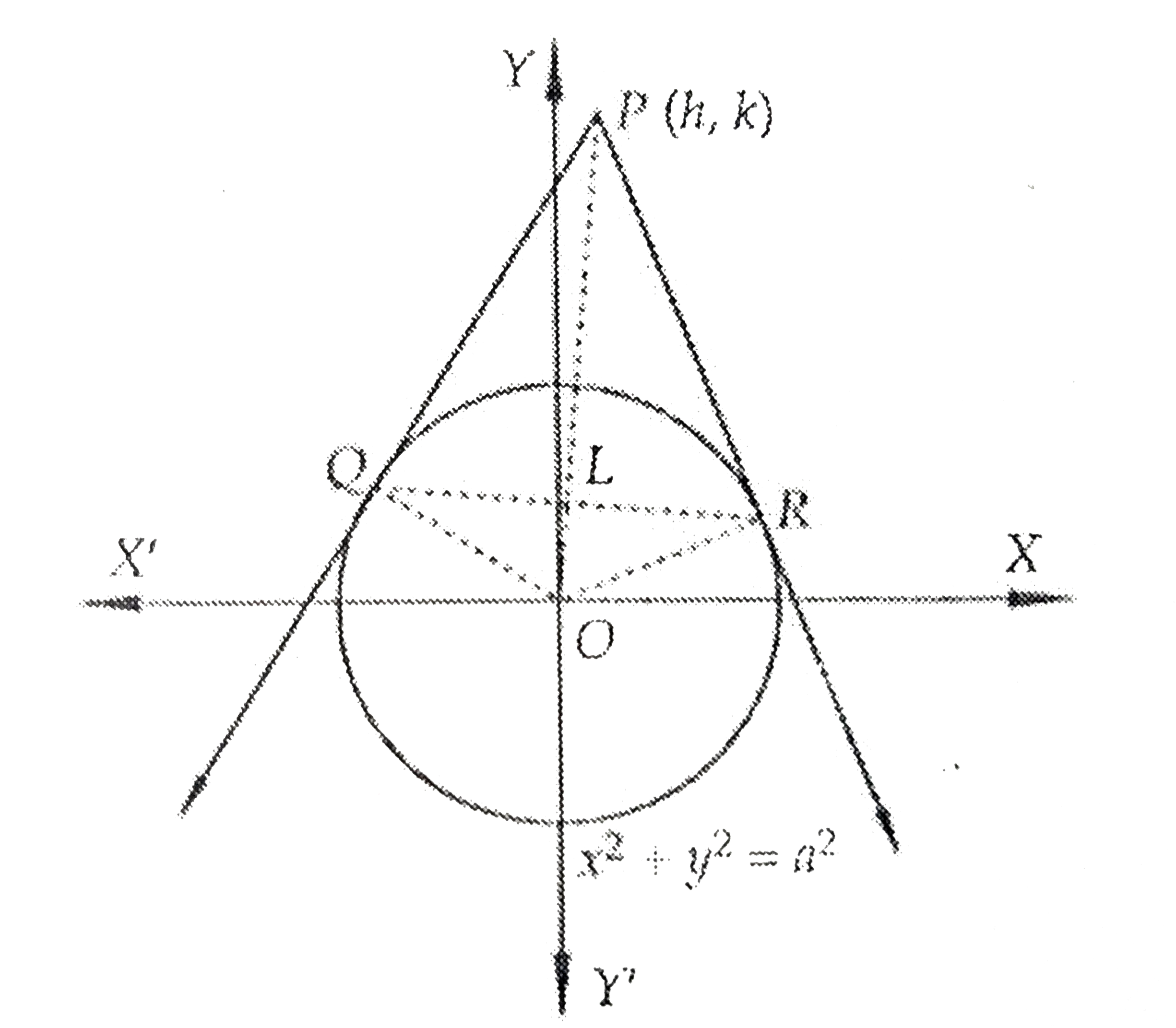
Now,
PL = Length of perpendicular from P(h, k) to (ii)
`rArr PL=|(h^(2)+k^(2)-a^(2))/(sqrt(h^(2)+k^(2)))|`
`rArrPL=(h^(2)+k^(2)-a^(2))/(sqrt(h^(2)+k^(2)))[[:'P(h, k) "lies outside"x^(2)+y^(2)=a^(2)],[:.h^(2)+k^(2)-a^(2)gt 0]]`
`:. OL=OP-PL=sqrt(h^(2)+k^(2))-(h^(2)+k^(2)-a^(2))/(sqrt(h^(2)+k^(2)))=(a^(2))/(sqrt(h^(2)+k^(2)))`
In `DeltaOLR`, we have
`LR=sqrt(OR^(2)-OL^(2))=sqrt(a^(2)-(a^(4))/(h^(2)+k^(2)))=asqrt((h^(2)+k^(2)-a^(2))/(h^(2)+k^(2)))`
`:. QR=2LR=2asqrt((h^(2)+k^(2)-a^(2))/(h^(2)+k^(2)))`
`:.` Area of `DeltaPQR=(1)/(2)(QRxxPL)=(a(h^(2)+k^(2)-a^(2))^(3//2))/(h^(2)+k^(2))`