There are two circles C1 and C2 touching each other and the coordinate axes, if C1 is smaller than C2 and its radius is 2 units, then radius of C2, is
6+4√2
2+2√2
3+2√2
none of these
The correct Answer is:A
To solve the problem, we need to find the radius of the larger circle C2 given that the radius of the smaller circle C1 is 2 units. Both circles touch each other and the coordinate axes.
1. Understanding the Configuration:
- Let the radius of circle C1 be r1=2 units.
- Let the radius of circle C2 be r2 (which we need to find).
- Both circles touch each other and the coordinate axes.
2. Positioning the Circles:
- Circle C1 can be positioned with its center at (2,2) since it touches both the x-axis and y-axis.
- Circle C2 will have its center at (r2,r2) since it also touches both axes.
3. Distance Between the Centers:
- The distance between the centers of the two circles C1 and C2 can be calculated using the distance formula:
Distance=√(r2−2)2+(r2−2)2=√2(r2−2)2=√2|r2−2|
4. Condition for Touching Circles:
- For the circles to touch each other, the distance between their centers must equal the sum of their radii:
√2|r2−2|=r1+r2=2+r2
- This simplifies to:
√2|r2−2|=2+r2
5. Solving the Equation:
- We can consider two cases for |r2−2|:
- Case 1: r2−2≥0 (i.e., r2≥2):
√2(r2−2)=2+r2
√2r2−2√2=2+r2
(√2−1)r2=2+2√2
r2=2+2√2√2−1
- Case 2: r2−2<0 (i.e., r2<2):
√2(2−r2)=2+r2
2√2−√2r2=2+r2
(1+√2)r2=2√2−2
r2=2(√2−1)1+√2
6. Calculating the Radius:
- We will only consider the first case since C2 is larger than C1:
r2=2+2√2√2−1
- Rationalizing the denominator:
r2=(2+2√2)(√2+1)(√2−1)(√2+1)=(2√2+2+4+2√2)2−1=6+4√2
Final Answer:
The radius of circle C2 is 6+4√2 units.
---
- Let the radius of circle C1 be r1=2 units.
- Let the radius of circle C2 be r2 (which we need to find).
- Both circles touch each other and the coordinate axes.
- Circle C1 can be positioned with its center at (2,2) since it touches both the x-axis and y-axis.
- Circle C2 will have its center at (r2,r2) since it also touches both axes.
- The distance between the centers of the two circles C1 and C2 can be calculated using the distance formula:
Distance=√(r2−2)2+(r2−2)2=√2(r2−2)2=√2|r2−2|
- For the circles to touch each other, the distance between their centers must equal the sum of their radii:
√2|r2−2|=r1+r2=2+r2
- This simplifies to:
√2|r2−2|=2+r2
- We can consider two cases for |r2−2|:
- Case 1: r2−2≥0 (i.e., r2≥2):
√2(r2−2)=2+r2
√2r2−2√2=2+r2
(√2−1)r2=2+2√2
r2=2+2√2√2−1
√2(2−r2)=2+r2
2√2−√2r2=2+r2
(1+√2)r2=2√2−2
r2=2(√2−1)1+√2
- We will only consider the first case since C2 is larger than C1:
r2=2+2√2√2−1
- Rationalizing the denominator:
r2=(2+2√2)(√2+1)(√2−1)(√2+1)=(2√2+2+4+2√2)2−1=6+4√2
The radius of circle C2 is 6+4√2 units.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
Two circles C1 and C2 intersect in such a way that their common chord is of maximum length. The center of C1 is (1, 2) and its radius is 3 units. The radius of C2 is 5 units. If the slope of the common chord is 34, then find the center of C2.
View SolutionThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
View SolutionThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
View SolutionThe two circles x2+y2=ax,x2+y2=c2(c>0) touch each other if
View SolutionC1 is a circle of radius 1 touching the x- and the y-axis. C2 is another circle of radius greater than 1 and touching the axes as well as the circle C1 . Then the radius of C2 is (a)3−2√2 (b) 3+2√2 3+2√3 (d) none of these
View SolutionConsider circles C1andC2 touching both the axes and passing through (4,4), then the product of the radii of the two circles is
View SolutionThe two circles x2+y2=axandx2+y2=c2(c>0) touch each other, if ∣∣ca∣∣ is equal to
View SolutionThe tangent to the circle C1:x2+y2−2x−1=0 at the point ( 2,1) cuts off a chord of length 4 from a circle C2 whose centre is(3,−2) . The radius of C2is :
View SolutionShows these variation of charge q for two capacitors C1 and C2 The two capacitors have the same plate separation. But the plate area of C2 is double than that of C1. Which of the lines in the figure corresponds to C1 and C2 and why?
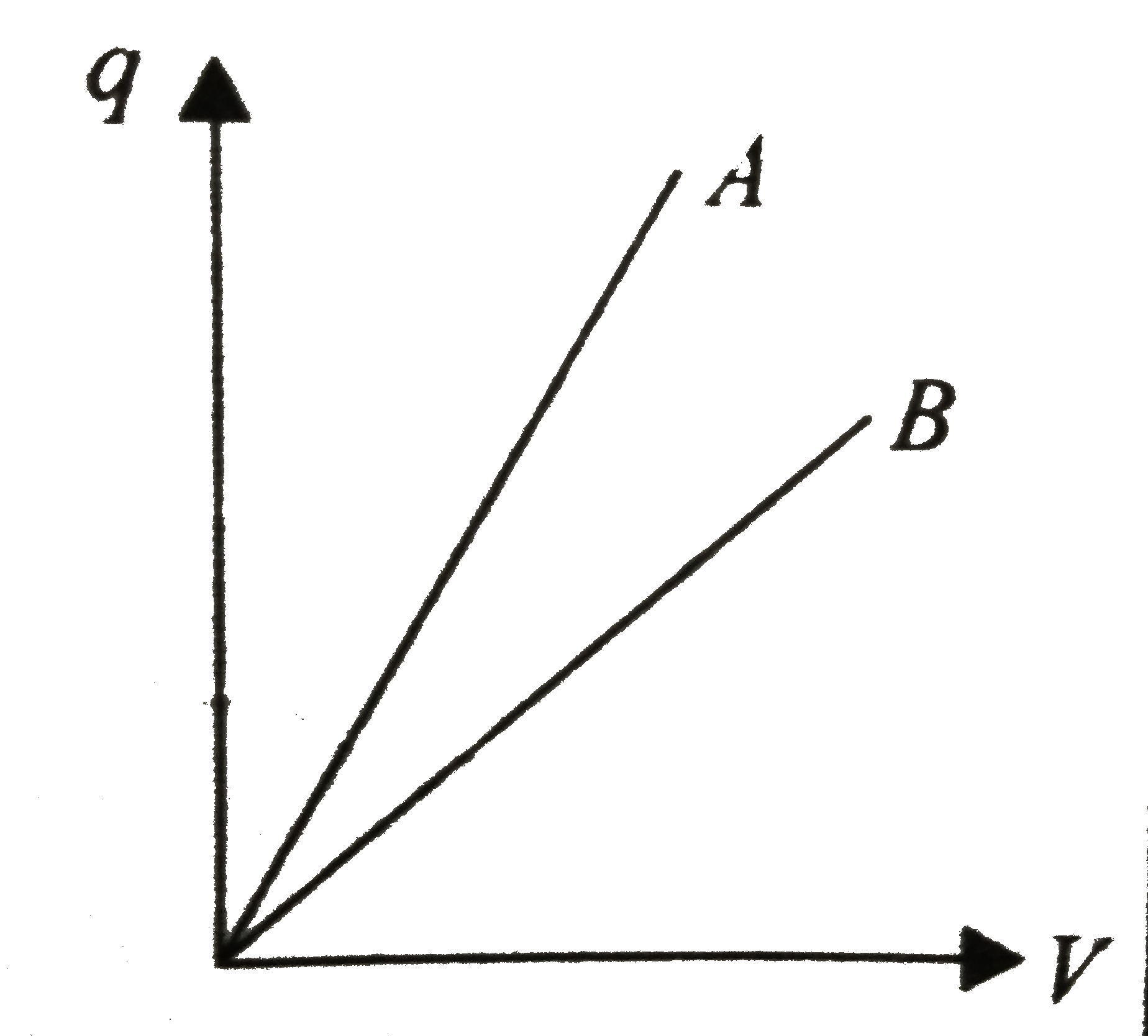 .
.
View SolutionStatement-1: The centre of the circle passing through the points (0, 0), (1, 0) and touching the circle C:x2+y2=9 lies inside the circle.
Statement-2: If a circle C1 passes through the centre of the circle C2 and also touches the circle, the radius of the circle C2 is twice the radius of circle C1
View Solution
