If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is

A

$x^{2} + y^{2} = k^{2}$

B

$x^{2} + y^{2} = 2 k^{2}$

C

$x^{2} + y^{2} = 3 k^{2}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let the coordinates of A and B be (a, 0) and (0, b) respectively . Clearly, $Δ O A B$ is a right-angled triangle, the hypotenuse AB is a diameter of the circle.

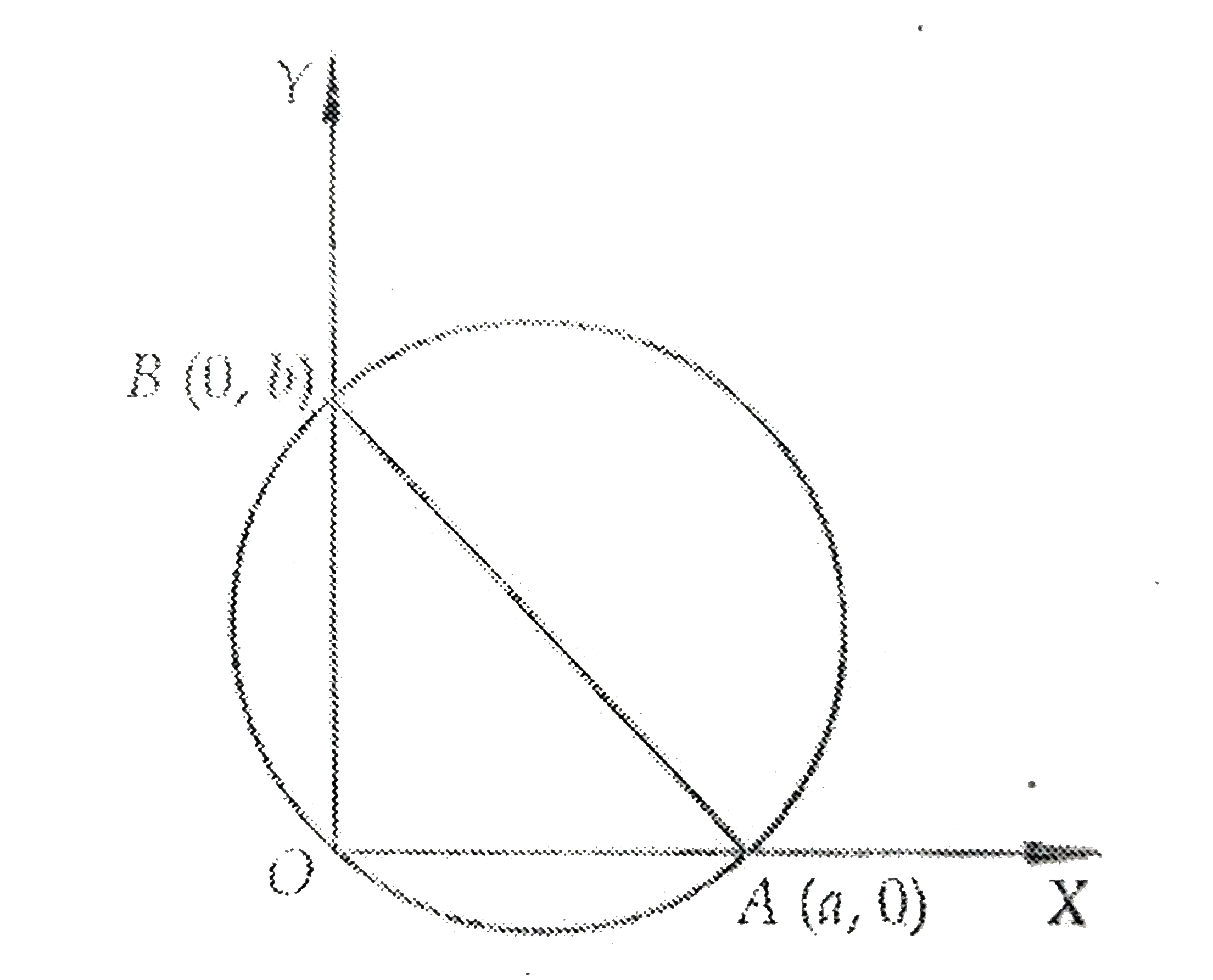
$∴ A B = 2 (3 k) = 6 k$ .
Now, $O A^{2} + O B^{2} = A B^{2} \Rightarrow a^{2} + b^{2} = 36 k^{2} ... (i)$
Let $(α, β)$ be the coordinates of the centroid of $Δ O A B$ . Then,
$α = a / 3, β = b / 3 \Rightarrow a = 3 α, b = 3 β$ .
Substituting the value of a and b in (i), we get
$9 α^{2} + 9 β^{3} = 36 k^{2} \Rightarrow α^{2} + β^{2} = 4 k^{2}$
Hence, the locus of $(α, β)$ is $x^{2} + y^{2} = 4 k^{2}$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

OBJECTIVE RD SHARMA ENGLISH-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile