The number of points with integral coordinates that are interior to the circle x2+y2=16, is
43
49
45
51
The correct Answer is:C
The circle cuts the cordinates axes at (-4, 0), (4,0), (0, 4) and (0, -4). So, the number of point is equal to the number of integral solutions , (x, y) such that x2+y2<16, where −4<x<4 and −4<y<4
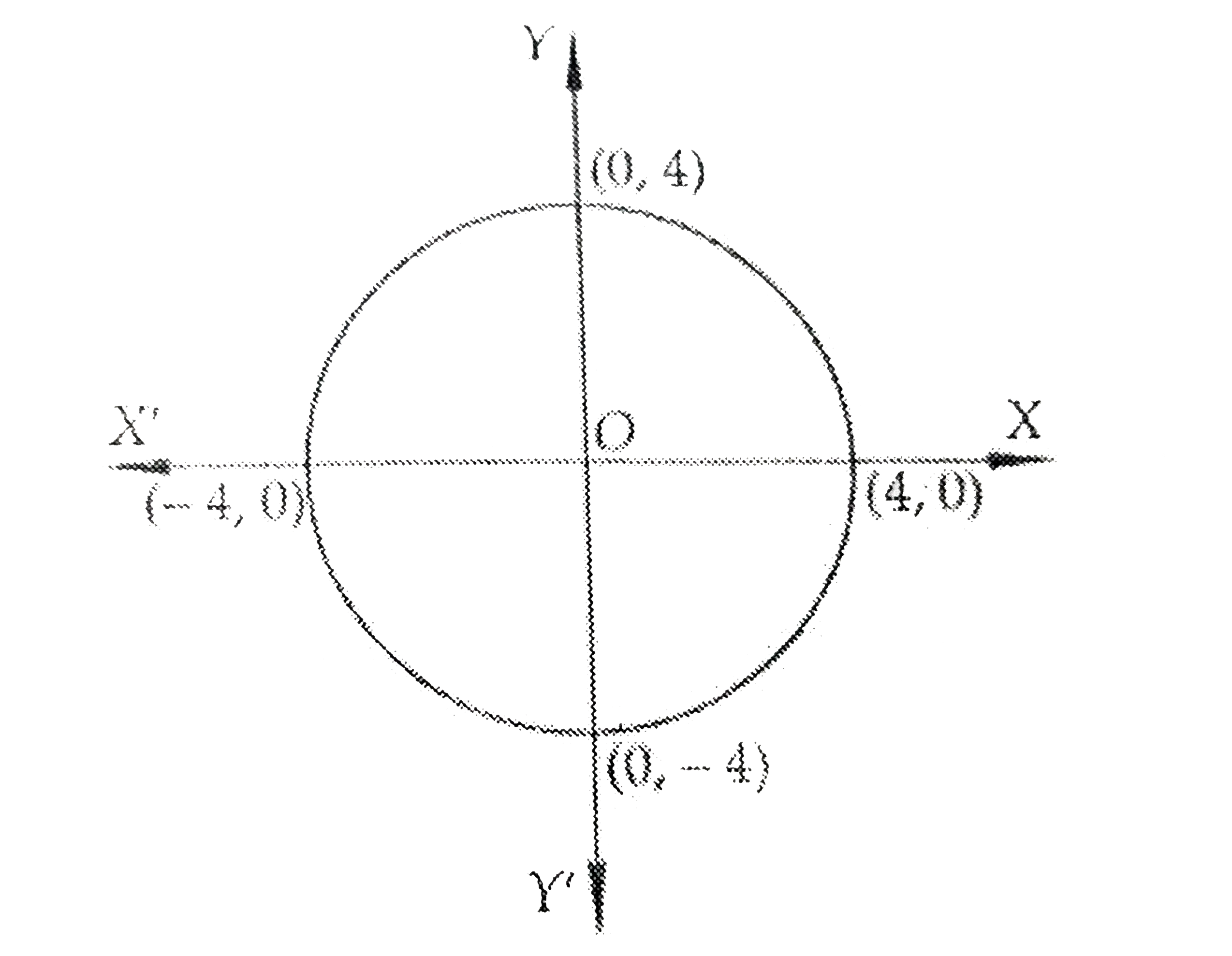
i.e., x∈[−3,3] and y∈[−3,3]
Clearly, x and y each can take 7 integral values, namely, -3, -2, -1, 0, 1, 2, 3. So, the number of ordered pairs (x, y) is 7 xx 7 = 49.<br>But,outofthese49orderedpairs(3,3),(−3,3),(−3,−3)and(3,−3)do¬satiyx^(2) + y^(2) lt 16.
Hence, required number of ordered pairs = 45.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
The number of points with integral coordinates that lie in the interior of the region common to the circle x2+y2=16 and the parabola y2=4x, is
View SolutionThe centre of circle (x+2)2+(y+4)2=16
View SolutionFind the number of point (x,y) having integral coordinates satisfying the condition x2+y2<25
View SolutionThe range of values of θ∈[0,2π] for which (1+cosθ,sinθ) is on interior point of the circle x2+y2=1, is
View SolutionThe Centre of Circle: (x+2)2+(y+4)2=16 is
View SolutionIf point P(x,y) is called a lattice point if x,y∈I. Then the total number of lattice points in the interior of the circle x2+y2=a2,a≠0 can not be:
View SolutionFind the number of integral points which lie on or inside the circle x2+y2=4.
View SolutionThe area of the triangle formed by the tangent at the point (a, b) to the circle x2+y2=r2 and the coordinate axes, is
View SolutionThe area of the triangle formed with coordinate axes and the tangent at (x1,y1) on the circle x2+y2=a2 is
View SolutionFind the center of circle
(x+2)2+(y+4)2=16
View Solution
