A chord of the circle x2+y2=a2 cuts it at two points A and B such that ∠AOB=π/2, where O is the centre of the circle. If there is a moving point P on this circle, then the locus of the orthocentre of ΔPAB will be a
parabola
circle
straight line
none of these
The correct Answer is:B
To solve the problem, we need to find the locus of the orthocenter of triangle PAB where P is a moving point on the circle defined by the equation x2+y2=a2, and A and B are points on the circle such that ∠AOB=π2.
1. Identify the Circle and Points:
The equation of the circle is given by:
x2+y2=a2
The center of the circle O is at the origin (0,0).
2. Determine Points A and B:
Since ∠AOB=π2, points A and B are at right angles to each other. We can choose:
A=(a,0)andB=(0,a)
3. Moving Point P:
Let P be a point on the circle with coordinates (h,k) such that:
h2+k2=a2
4. Find the Orthocenter of Triangle PAB:
The orthocenter H of triangle PAB can be found using the properties of the triangle. The circumcenter C of triangle PAB is at the origin O(0,0).
5. Centroid of Triangle PAB:
The coordinates of the centroid G of triangle PAB are given by:
G=(h+a+03,k+0+a3)=(h+a3,k+a3)
6. Relationship Between Orthocenter, Centroid, and Circumcenter:
The centroid G divides the line segment joining the orthocenter H and the circumcenter C in the ratio 2:1:
G=2H+C3
Since C is at the origin (0,0), we have:
G=2H3
7. Setting Up the Equations:
From the coordinates of G:
h+a3=2α3andk+a3=2β3
This gives us:
h+a=2αandk+a=2β
Rearranging gives:
h=2α−aandk=2β−a
8. Substituting into the Circle Equation:
Substitute h and k into the equation of the circle:
(2α−a)2+(2β−a)2=a2
Expanding this:
4α2−4aα+a2+4β2−4aβ+a2=a2
Simplifying gives:
4α2+4β2−4a(α+β)+a2=0
Rearranging leads to the equation:
α2+β2−a(α+β)+a24=0
9. Identifying the Locus:
This equation represents a circle with center at (a/2,a/2) and radius a.
Conclusion:
The locus of the orthocenter of triangle PAB as point P moves around the circle x2+y2=a2 is a circle centered at (a,a) with radius a.
The equation of the circle is given by:
x2+y2=a2
The center of the circle O is at the origin (0,0).
Since ∠AOB=π2, points A and B are at right angles to each other. We can choose:
A=(a,0)andB=(0,a)
Let P be a point on the circle with coordinates (h,k) such that:
h2+k2=a2
The orthocenter H of triangle PAB can be found using the properties of the triangle. The circumcenter C of triangle PAB is at the origin O(0,0).
The coordinates of the centroid G of triangle PAB are given by:
G=(h+a+03,k+0+a3)=(h+a3,k+a3)
The centroid G divides the line segment joining the orthocenter H and the circumcenter C in the ratio 2:1:
G=2H+C3
Since C is at the origin (0,0), we have:
G=2H3
From the coordinates of G:
h+a3=2α3andk+a3=2β3
This gives us:
h+a=2αandk+a=2β
Rearranging gives:
h=2α−aandk=2β−a
Substitute h and k into the equation of the circle:
(2α−a)2+(2β−a)2=a2
Expanding this:
4α2−4aα+a2+4β2−4aβ+a2=a2
Simplifying gives:
4α2+4β2−4a(α+β)+a2=0
Rearranging leads to the equation:
α2+β2−a(α+β)+a24=0
This equation represents a circle with center at (a/2,a/2) and radius a.
The locus of the orthocenter of triangle PAB as point P moves around the circle x2+y2=a2 is a circle centered at (a,a) with radius a.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
A circle touches x-axis and cuts off constant length 2p from y-axis then the locus of its centre is
View SolutionTwo tangents are drawn from any point P on a given line L=0 to a given circle S=0, if these tangents touch the circle at point A and B, then locus of the circumcentre the ΔPAB will be
View Solution
Knowledge Check
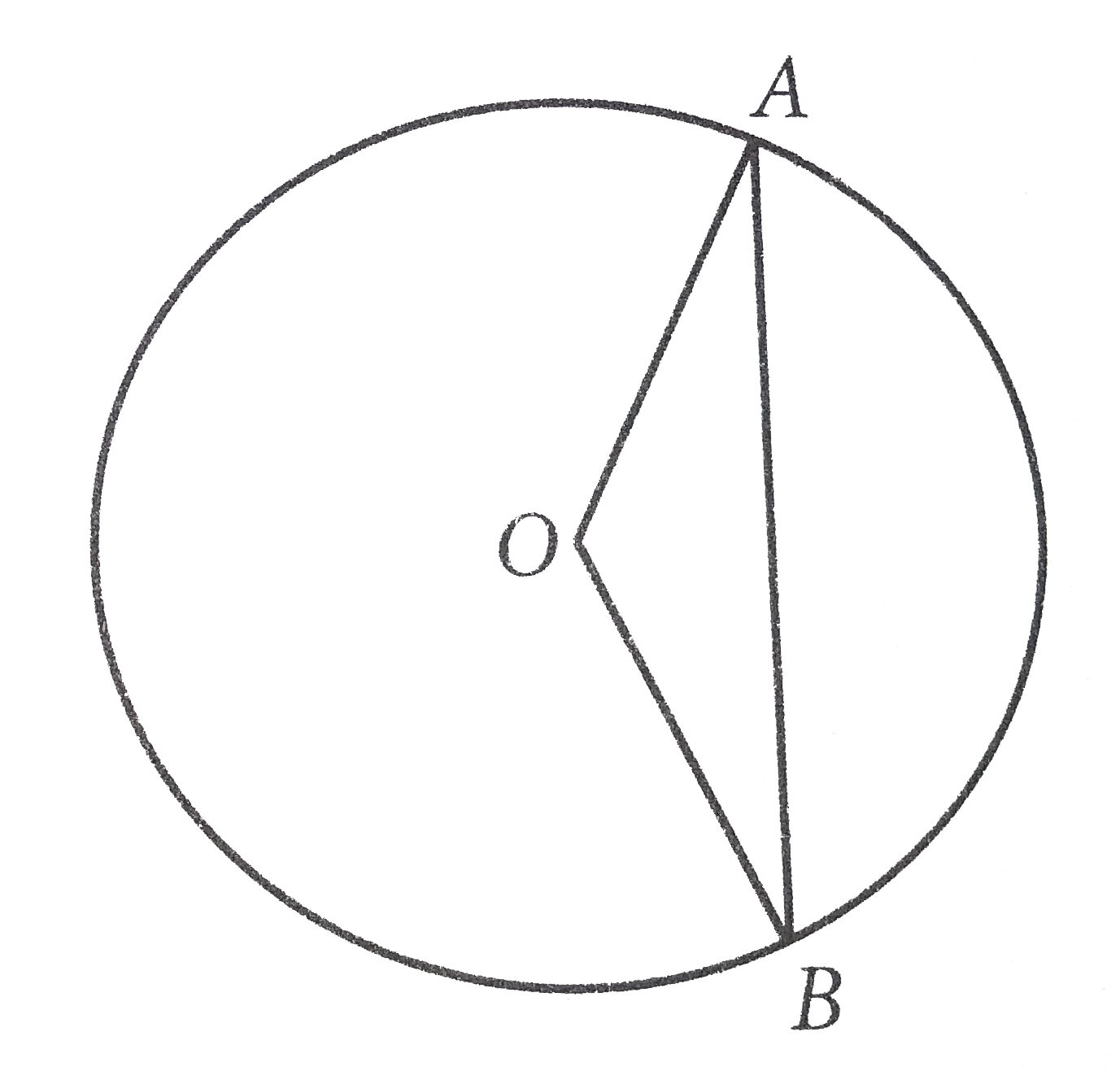
If the radius of the circle above is x, ∠AOB=120∘, and O is the center of the circle, what is the length of chord AB, in terms of x?A√2xB√3xCx√2Dx√3
Two tangents to the circle x2+y2=4 at the points A and B meet at P(−4,0), The area of the quadrilateral PAOB, where O is the origin, is
View SolutionIf a circle Passes through a point (1,2) and cut the circle x2+y2=4 orthogonally,Then the locus of its centre is
View SolutionIf a circle Passes through a point (1,0) and cut the circle x2+y2=4 orthogonally,Then the locus of its centre is
View SolutionIf a circle passes through the point (a,b) and cuts the circle x2+y2=k2 orthogonally then the locus of its centre is
View SolutionIf a circle passes through the point (a,b) and cuts the circlex x2+y2=p2 equation of the locus of its centre is
View SolutionIf from the origin a chord is drawn to the circle x2+y2−2x=0, then the locus of the mid point of the chord has equation
View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
View Solution
