The locus of the mid-points of the chords of the circle of lines radiùs r which subtend an angle at any point on the circumference of the circle is a concentric circle with radius equal to (a) (b) (c) (d)
The correct Answer is:C
Let P(h,k) be the mid-point of the chord subtending angle at the centre.
In , we have
Locus of (h,k) is .
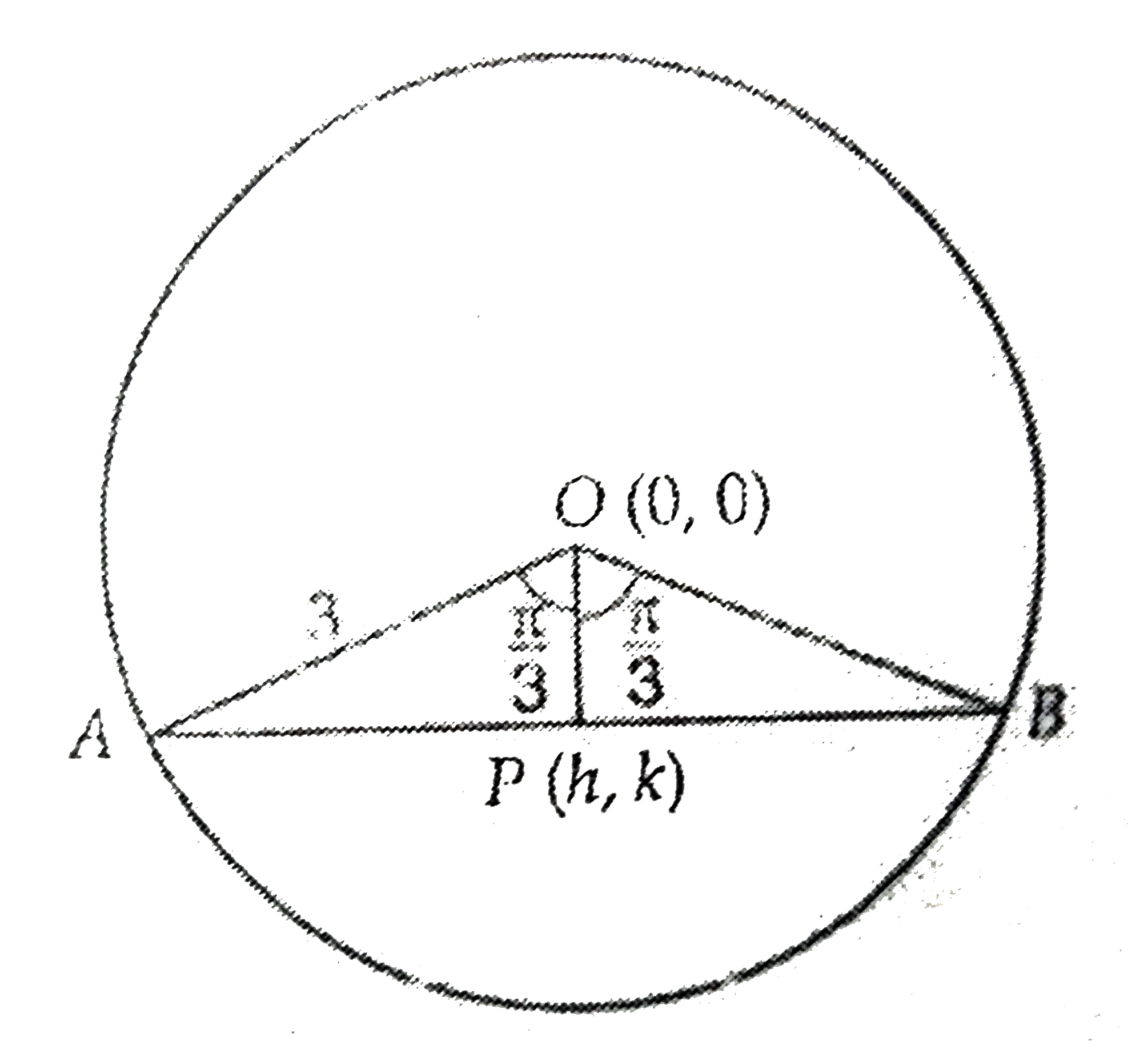
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type12videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test53videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test30videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
Similar Questions
The locus of the mid-points of the chords of the circle x2+y2−2x−4y−11=0 which subtends an angle of 60∘ at center is
View SolutionFind the locus of the mid-point of the chords of the circle x2+y2+2gx+2fy+c=0 which subtend an angle of 1200 at the centre of the circle.
View SolutionFind the equation of the circle in which the chord joining the points (a,b)and(b,−a) subtends an angle of 45∘ at any point on the circumference of the circle.
View SolutionThe length of the common chord of two circles of radii r1 and r2 which intersect at right angles is
View SolutionIf a chord AB of a circle subtends an angle θ(≠π/3) at a point C on the circumference such that the triangle ABC has maximum area , then
View SolutionThe locus of the point, the chord of contact of which wrt the circle x2+y2=a2 subtends a right angle at the centre of the circle is
View SolutionIf the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then
View SolutionWrite expression for circumference of a circle of radius 'r'
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals
View SolutionThe locus of the point, whose chord of contact w.r.t the circle x2+y2=a2 makes an angle 2α at the centre of the circle is
View Solution

