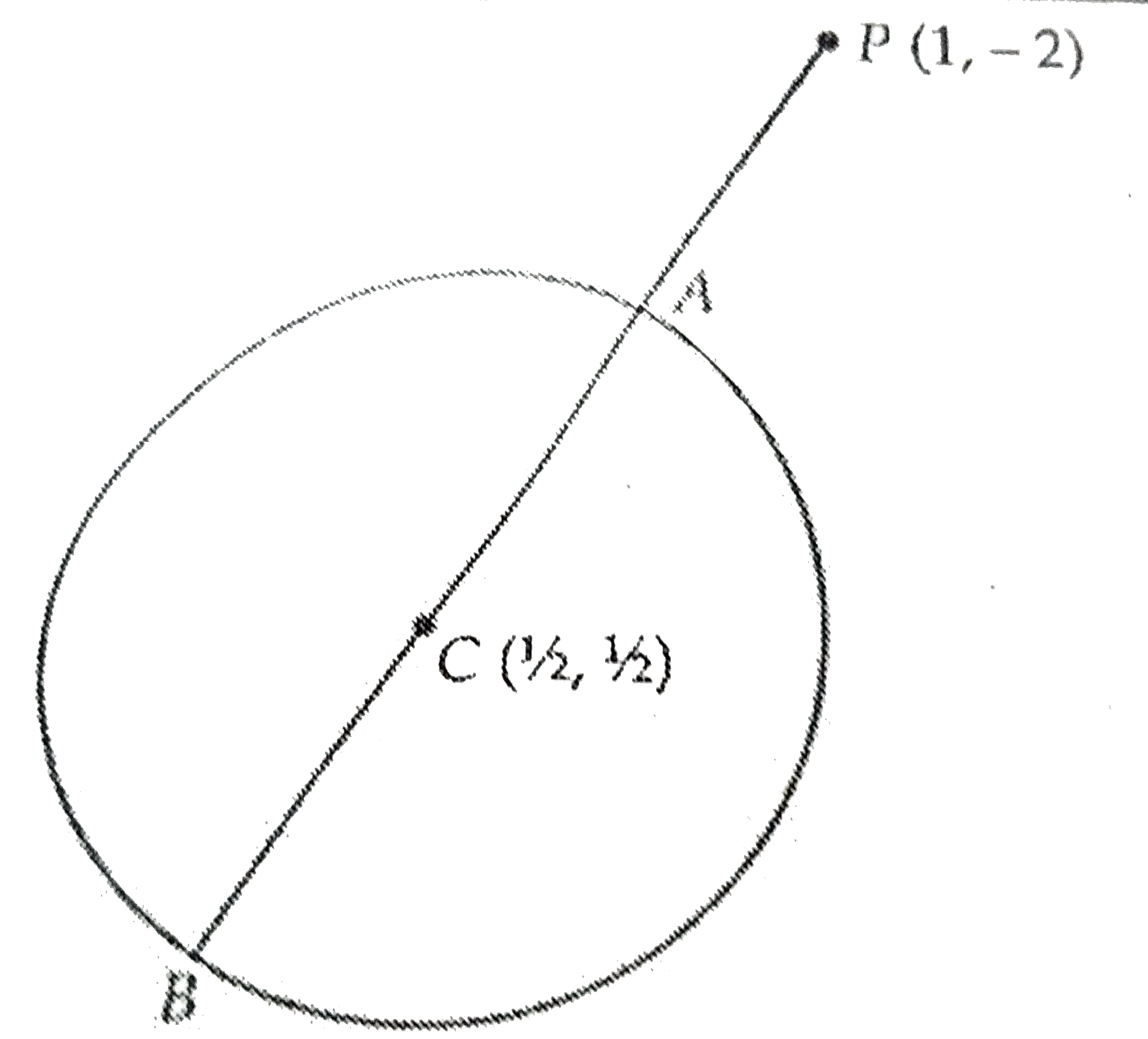
If a line passes through the point P(1,-2) and cuts the circle x2+y2−x−y=0 at A and B, then the maximum value of PA+PB is
√a
8
√8
2√8
The correct Answer is:A
We have, PA+ PAB = 2 PA+AB
Clearly, PA + PB is maximum when AB is maximum i.e. AB isa diameter of the circle.
Now,
PA+PB=(PC-AC)+(PC+CB)
⇒PPB=2PC [∵AC=CB]
⇒PA+PB=2√14+254=√26
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
If a line passes through the point P(1,−2) and cuts the x2+y2−x−y=0at A and B, then themaxiμmofPA+PB is
View SolutionA line is drawn through the point P(3,11) to cut the circle x2+y2=9 at A and B. Then PA.PB is equal to
View SolutionIf a circle passes through the point (1, 1) and cuts the circle x2+y2=1 orthogonally, then the locus of its centre is
View SolutionIf a circle passes through the point (a,b) and cuts the circle x2+y2=k2 orthogonally, then the equation of the locus of its center is
View SolutionIf the line passing through P=(8,3) meets the circle S≡x2+y2−8x−10y+26=0 at A,B then PA.PB=
View SolutionIf a circle passes through the point (a,b) and cuts the circlex x2+y2=p2 equation of the locus of its centre is
View SolutionIf a circle passes through the point (a,b) and cuts the circle x2+y2=k2 orthogonally then the locus of its centre is
View SolutionIf a circle passes through the point (a,b) and cuts the circle x2+y2=k2 orthogonally , show that the locus of its centre is 2ax+2by−(a2+b2+k2)=0
View SolutionIf a circle Passes through a point (1,2) and cut the circle x2+y2=4 orthogonally,Then the locus of its centre is
View SolutionIf a line through P(-2,3) meets the circle x2+y2−4x+2y+k=0 at A and B such that PA.PB=31 then the radius of the circles is
View Solution
