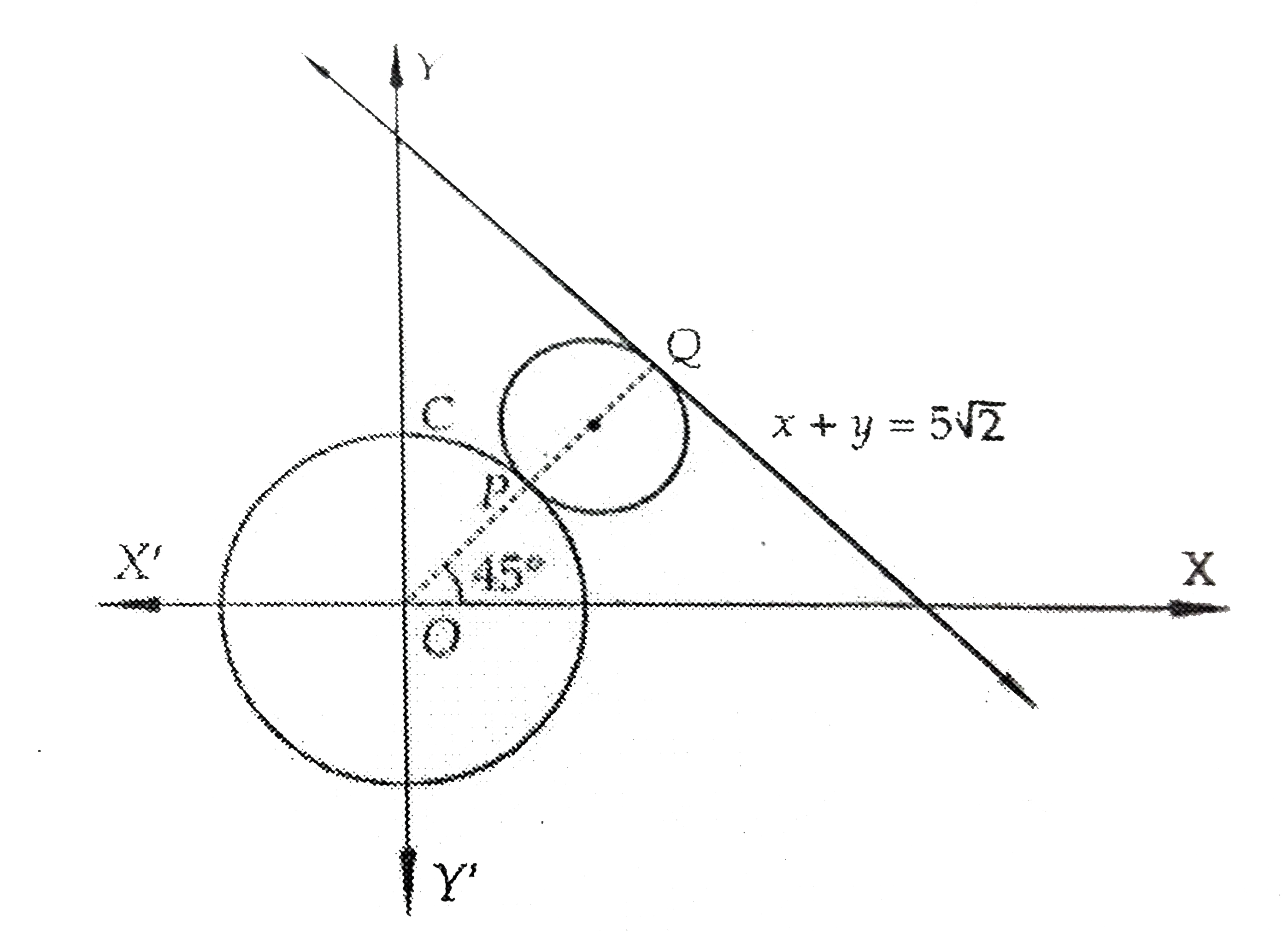
The equation of a circle is $x^{2} + y^{2} = 4 .$ Find the center of the smallest circle touching the circle and the line $x + y = 5 \sqrt{2}$

A

$(\frac{7}{2 \sqrt{2}}, \frac{7}{2 \sqrt{2}})$

B

$(\frac{3}{2}, \frac{3}{2})$

C

$(- \frac{7}{2 \sqrt{2}}, - \frac{7}{2 \sqrt{2}})$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We have, OP=2 and OQ=5.
$∴ C P = C Q = \frac{3}{2} \Rightarrow O C = 2 + \frac{3}{2} = \frac{7}{2}$
The equation of OC is $\frac{x - 0}{\frac{1}{\sqrt{2}}} = \frac{y - 0}{\frac{1}{\sqrt{2}}} = \frac{7}{2} \Rightarrow x = y = \frac{7}{2 \sqrt{2}}$
Hence, the coordinates of C are $(\frac{7}{2 \sqrt{2}}, \frac{7}{2 \sqrt{2}})$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

OBJECTIVE RD SHARMA ENGLISH-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile