The number of real solutions (x, y), where |y|=sinx,y=cos−1(cosx),−2π≤x≤2π, is :
2
1
3
4
The correct Answer is:C
Graph of |y| =sin x and y = cos−1 are shown in fig 19 it is evident form the graph that the curves inersect at (0,0)(2,π,0) and (−2π,0) hence there are 3 solution
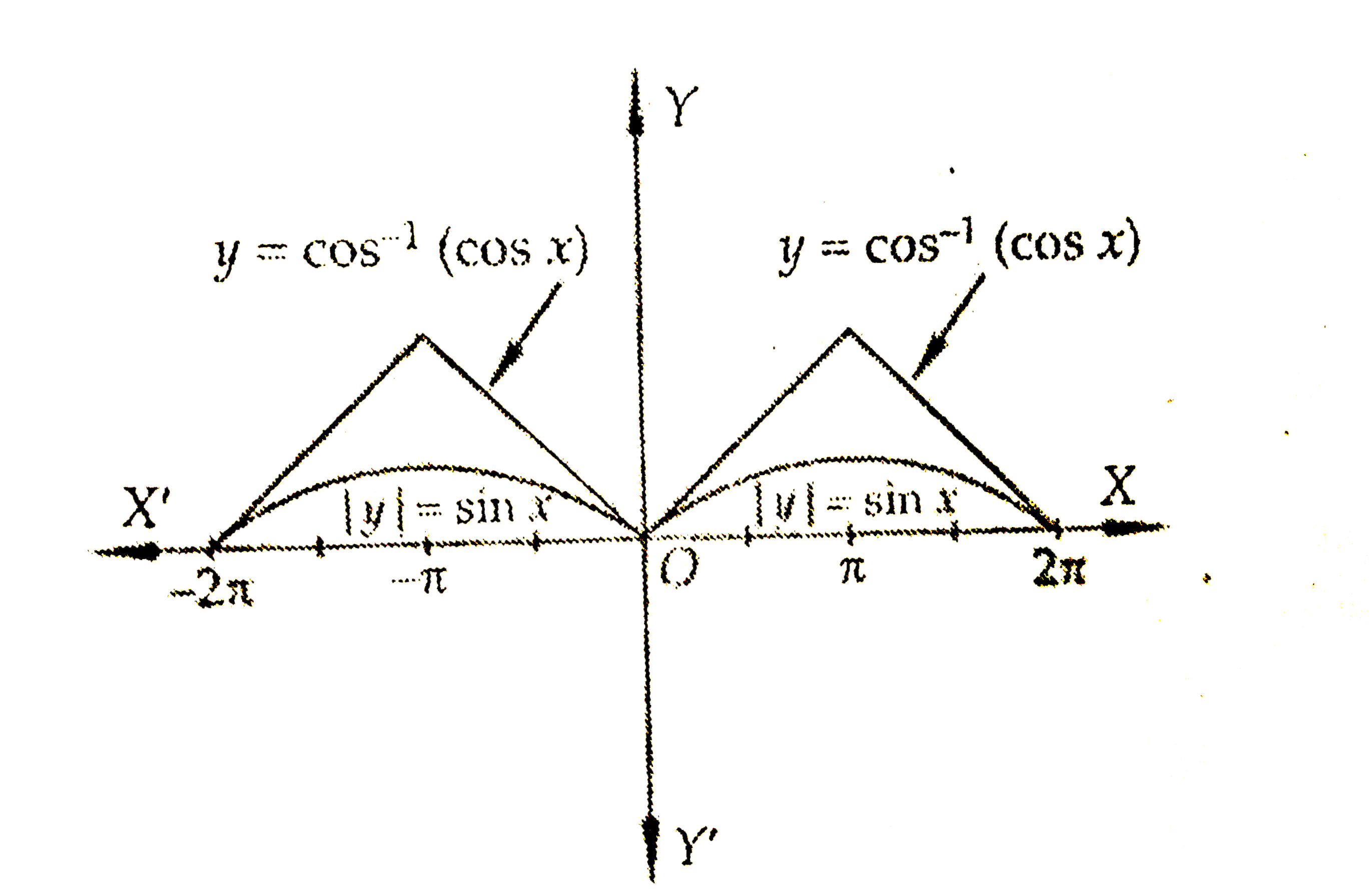
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Section II - Assertion Reason Type
11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise
72 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test
30 Videos
- INDEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INDEFINITE INTEGRALSEXERCISE - Chapter Test
30 Videos
- LIMITSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LIMITSEXERCISE - Chapter Test
58 Videos
Similar Questions
The number of real solutions (x,y), where |y|=sinx,y=cos−1(cosx),−2π≤x≤2π is
View SolutionThe number of real solution of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π, is
View SolutionThe number of real solution of the equation √1+cos2x=√2sin−1(sinx),−π≤x≤π, is
View SolutionFind the number of solution of the equation |y|=sinxandy=cos−1cosx where −2π≤x≤2π
View SolutionThe number of solutions of the equation |y|=cosxandy=cot−1(cotx) in (−3π2,5π2) is
View SolutionThe number of points of intersection of the curves 2y=1 and y=sinx,−2π≤x≤2π, is
View SolutionDraw the graph of y=sinx and y=cosx,0≤x≤2π
View SolutionSolve the equation (sinx+cosx)1+sin2x=2 , when −π≤x≤π .
View SolutionFind the number of solutions of |cosx|=sinx,0≤x≤4π
View SolutionThe total number of ordered pairs (x, y) satisfying |y|=cosxandy=sin−1(sinx), where x∈[−2π,3π] is equal to :
View Solution
