Question

If $f\left(x\right)=\underset{0}{\stackrel{x}{\int }}{e}^{t^2}(t-2)(t-3)dt$ for all $x\in (0,\infty )$ , then

Options

A. f has a local maximum at x=2 and local minimum at x=3
B. f is dereasing on (2,3)
C. there exists ` c in (0,oo) " such that f " ( c)=0`
D. f is inceresing on `R^+`

Answer

D

Explanation

We have
`f(x)=underset(0)overset(x)int e^(6^2)(t-2)(t-3)dt`
`rArr f(x)=e^(x^2)(x-2)(x-3)`
The chages in sings of f(x) for different values of x are as given below :

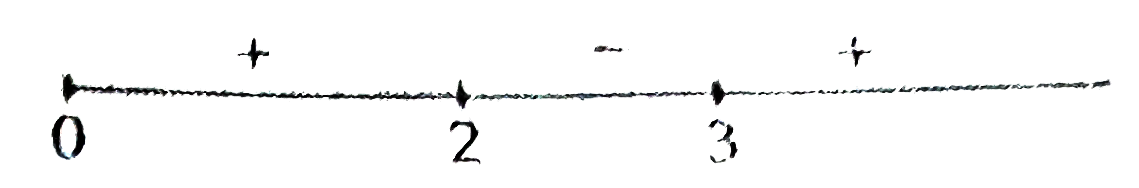
Clearly `f(x) gt 0 " for " x in (0,2) cup (3,oo) " and f(x) lt 0 " for " ( x ) lt 0 `
`x in (2,3)` So f(x) is increasing on `(0,2) cup (3,oo)` and decreasing on (2,3).
As f(x) changes sign from positive as x passes through 2 and negatives to positive as x passes through 3. So, x=2 is point of local maximum and x=3 is a point of local minmum of f(x).
Clearly `f(x)=e^(x^2)(x-2)(x-3)` is continuous on [2,3] and differentiable on (2,3).Also f(2)=f(3)=0 .Therefore by Rolle's theorem there exists `c in (2,3)` such that f''(c) =0