If A(z1),B(z2)andC(z3) are three points in the argand plane where |z1+z2|=||z1−z2|and|(1−i)z1+iz3|=|z1|+|z3|−z1|, where i=√−1 then
A,B and C lie on a circle with center z2+z32
A,B and C are collinear points.
A,B,C from an equilateral triangle.
A,B,C form an obtuse angle triangle.
The correct Answer is:A
We have,
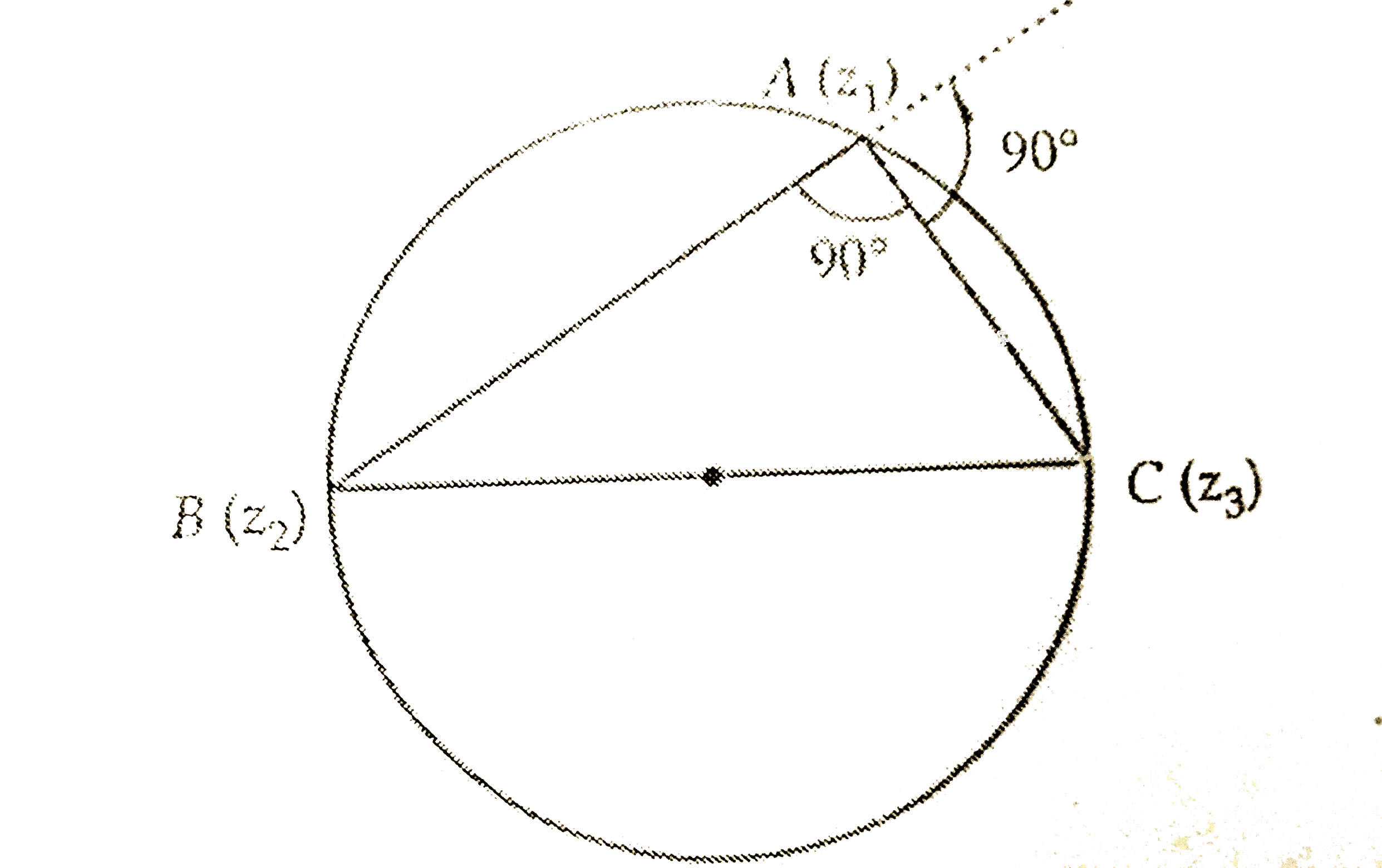
|z1+z2|=||z1|−|z2∣∣<⇒Arg(z1z2)=±π
and |(1−i)z1+iz3|=|z1|+|z3−z1|
<⇒|z1+i(z3−z1)|=|z1|+|z3−z1|
⇒arg(z1z3−z1=π2[∴|z1+iz2|=|z1|+|z2|<⇒arg(z1z2)=π2]
Thus, A lies on the circle with BC as diameter i.e., z2+z32 as center. Hence, option (a) is correct.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
129 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
Similar Questions
If A(z1),B(z2) and C(z3)are three points in the Argand plane such that z1+ωz2+ω2z3=0, then
View SolutionIf z1,z2andz3 are the vertices of a triangle in the argand plane such that |z1−z2|=|z1−z3|, then ∣∣∣arg(2z1−z2−z3z3−z2)∣∣∣ is
View SolutionThe points A(z1),B(z2)andC(z3) form an isosceles triangle in the Argand plane right angled at B, then z1−z2z3−z2 can be (A) 1 (B) -1 (C) −i (D) none of these
View SolutionIf z1,z2,z3,z4 are the affixes of four point in the Argand plane, z is the affix of a point such that |z−z1|=|z−z2|=|z−z3|=|z−z4| , then prove that z1,z2,z3,z4 are concyclic.
View SolutionIf z1,z2andz3, are the vertices of an equilateral triangle ABC such that |z1−i|=|z2−i|=|z3−i|.then |z1+z2+z3|equals:
View SolutionIf z1,z2,z3 are three collinear points in the argand plane such that |(z3−z1)(z3−z2)|=A2andz2−z3=λ.A2(z)1−(z)3, then value of |λ| is
View SolutionIf z1,z2,z3 are vertices of a triangle such that |z1−z2|=|z1−z3| then arg (2z1−z2−z3z3−z2) is :
View SolutionIf 2z1−3z2+z3=0, then z1,z2andz3 are represented by
View SolutionIf A(z1), B(z2), C(z3) are vertices of a triangle such that z3=z2−iz11−i and |z1|=3, |z2|=4 and |z2+iz1|=|z1|+|z2|, then area of triangle ABC is
View SolutionIf z1,z2,z3,z4 are the affixes of four point in the Argand plane, z is the affix of a point such that |z−z1|=|z−z2|=|z−z3|=|z−z4| , then z1,z2,z3,z4 are
View Solution