If z1 and z2 are the complex roots of the equation (x−3)3+1=0, then z1+z2 equal to
0≤d<152
0<d≤152
0≤d≤172
0<d<172
The correct Answer is:C
P(z1) and Q(z2) are points on the circle |z−3|≤4 and the ellipse |z−1|=|z+1|=3 respectively. The center of the circle is at (3,0) and radius 4. The center of the ellipse is at the origin and foci at S(1,0) and S′(−1,0). The major axis ∀′ is of length 3. Therefore, OA= OA′=32.
Clearly, d=PQ. The minimum value of d is 0 when P and Q coincide with L or M.
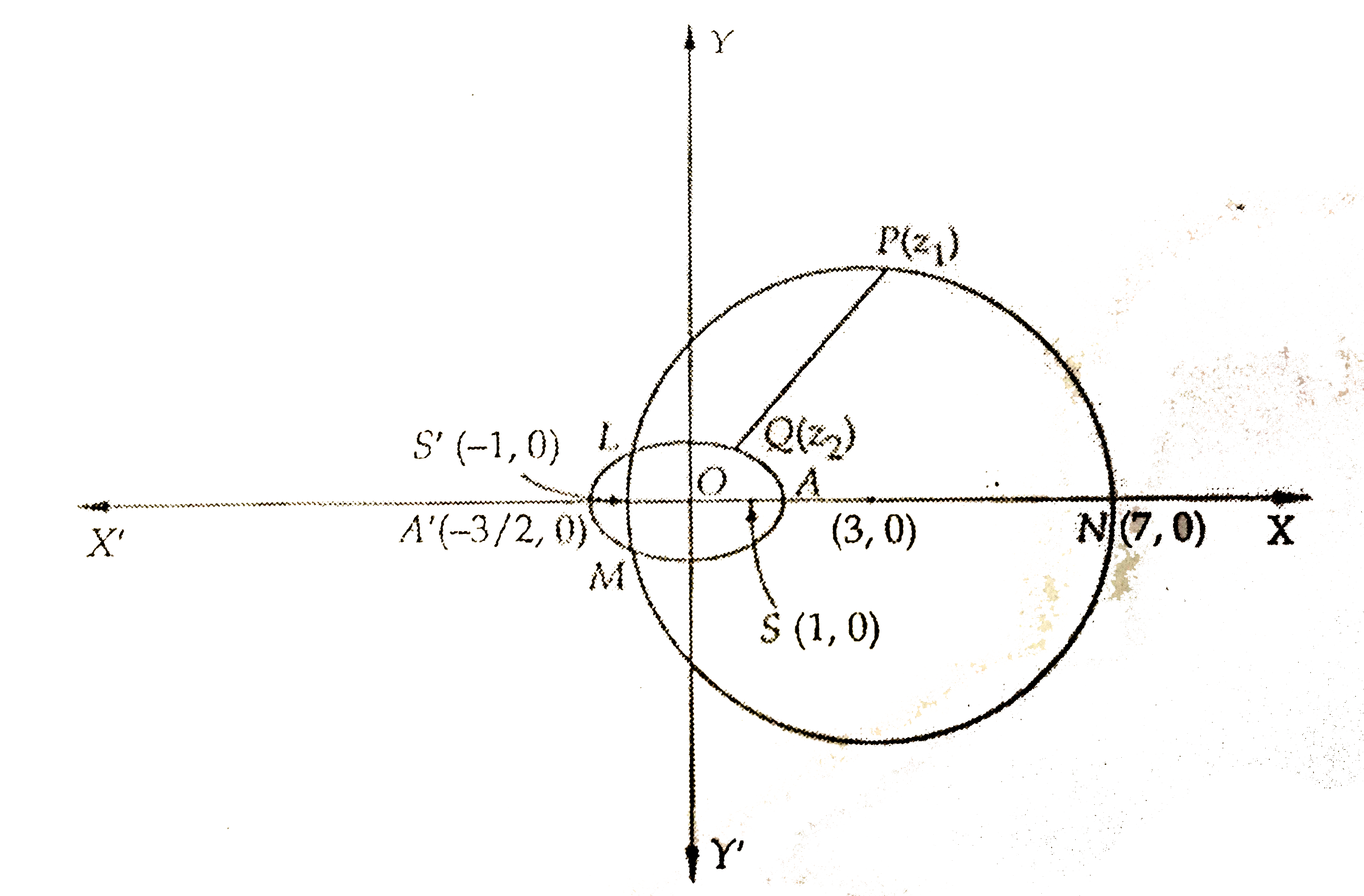
The maximum value of PQ is
A′N=OA′+ON=32+7=172
Hence, 0≤d≤172.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type15videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Exercise129videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test53videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise87videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
If z1andz2 are the complex roots of the equation (x−3)3+1=0,thenz1+z2 equal to 1 b. 3 c. 5 d. 7
View Solutionz1andz2 are the roots of the equaiton z2−az+b=0 where |z1|=|z2|=1 and a,b are nonzero complex numbers, then
View Solutionlet z1,z2,z3 and z4 be the roots of the equation z4+z3+2=0 , then the value of 4∏r=1(2zr+1) is equal to :
View SolutionIf z1,z2,z3 are any three roots of the equation z6=(z+1)6, then arg(z1−z3z2−z3) can be equal to
View SolutionSum of common roots of the equations z3+2z2+2z+1=0 and z1985+z100+1=0 is
View SolutionIf z1 and z2 are two complex numbers satisying the equation.
∣∣∣iz1+z2iz1−z2∣∣∣=1, then z1z2 isView SolutionIf z1andz2 are two complex numbers such that |z1|=|z2|, then is it necessary that z1=z2
View SolutionIf z1 and z2 are two complex numbers such that ∣∣∣z1−z2z1+z2∣∣∣=1, then
View SolutionCommon roots of the equation z3+2z2+2z+1=0 and z2020+z2018+1=0, are
View SolutionIf z1,z2 be two complex numbers satisfying the equation ∣∣∣z1+z2z1−z2∣∣∣=1, then
View Solution

