POQ is a straight line through the origin O,P and Q represent the complex numbers a+ib and c+id respectively and OP=OQ. Then, which one of the following is true?
|a+ib|=∣c+
a+b=c+d
arg(a+ib)=arg(c+id)
none of these
The correct Answer is:a
To solve the problem, we need to analyze the given conditions about the complex numbers representing points P and Q on the Argand plane.
1. Understanding the Points:
- Let P be represented by the complex number z1=a+ib.
- Let Q be represented by the complex number z2=c+id.
- Both points lie on a straight line through the origin O.
2. Distance from Origin:
- The distance from the origin O to point P is given by the modulus of z1, which is |z1|=|a+ib|.
- The distance from the origin O to point Q is given by the modulus of z2, which is |z2|=|c+id|.
3. Equality of Distances:
- We are given that OP=OQ. This means that the distances from the origin to points P and Q are equal:
|z1|=|z2|
- Therefore, we have:
|a+ib|=|c+id|
4. Magnitude Calculation:
- The magnitude of a complex number x+iy is calculated as:
|x+iy|=√x2+y2
- Applying this to our complex numbers:
|a+ib|=√a2+b2
|c+id|=√c2+d2
5. Setting the Magnitudes Equal:
- From the equality of distances, we can set up the equation:
√a2+b2=√c2+d2
6. Squaring Both Sides:
- To eliminate the square roots, we square both sides:
a2+b2=c2+d2
7. Conclusion:
- The condition that must hold true given the problem statement is:
a2+b2=c2+d2
- This means that the sum of the squares of the real and imaginary parts of z1 is equal to the sum of the squares of the real and imaginary parts of z2.
Final Answer:
The correct condition is a2+b2=c2+d2.
---
- Let P be represented by the complex number z1=a+ib.
- Let Q be represented by the complex number z2=c+id.
- Both points lie on a straight line through the origin O.
- The distance from the origin O to point P is given by the modulus of z1, which is |z1|=|a+ib|.
- The distance from the origin O to point Q is given by the modulus of z2, which is |z2|=|c+id|.
- We are given that OP=OQ. This means that the distances from the origin to points P and Q are equal:
|z1|=|z2|
- Therefore, we have:
|a+ib|=|c+id|
- The magnitude of a complex number x+iy is calculated as:
|x+iy|=√x2+y2
- Applying this to our complex numbers:
|a+ib|=√a2+b2
|c+id|=√c2+d2
- From the equality of distances, we can set up the equation:
√a2+b2=√c2+d2
- To eliminate the square roots, we square both sides:
a2+b2=c2+d2
- The condition that must hold true given the problem statement is:
a2+b2=c2+d2
- This means that the sum of the squares of the real and imaginary parts of z1 is equal to the sum of the squares of the real and imaginary parts of z2.
The correct condition is a2+b2=c2+d2.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
Similar Questions
Knowledge Check
The following diagram represents the solution of two sets P and Q on the number line:
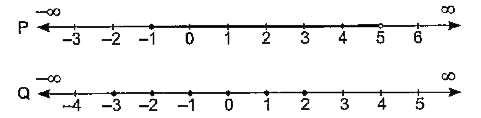
Which of the following is a replacement set of Q?ARBNCWDZThe five number 1056, 1098, 1100 and 1126 are represented on a number line by the point A, B, C, D and E, respectively, as shown in the figure. Which one of the following points represents the average of the five numbers ?
 APoint ABPoint BCPoint CDPoint D
APoint ABPoint BCPoint CDPoint D
Let OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents
View SolutionA straight line through the origin 'O' meets the parallel lines 4x+2y=9 and 2x+y=−6 at points P and Q respectively. Then the point 'O' divides the segment PQ in the ratio
View SolutionA straight line through origin O meets the lines 3y=10−4x and 8x+6y+5=0 at point A and B respectively. Then , O divides the Segment AB in the ratio.
View SolutionA straight line L through the origin meets the lines x+y=1 and x+y=3 at P and Q respectively. Through P and Q two straight lines L1, andL2 are drawn, parallel to 2x−y−5 and 3x+y5 respectively. Lines L1 and L2 intersect at R. Locus of R, as L varies, is
View SolutionConsider the set of all lines px+qy+r=0 such that 3p+2q+4r=0. Which one of the following statements is true ?
View SolutionA line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
View Solution
