A straight line through origin O meets the lines 3y=10−4x and 8x+6y+5=0 at point A and B respectively. Then , O divides the Segment AB in the ratio.
2:3
1:2
4:1
3:4
The correct Answer is:C
Step by step video & image solution for A straight line through origin O meets the lines 3y=10-4x and 8x+6y+5=0 at point A and B respectively. Then , O divides the Segment AB in the ratio. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Main Archive (State true or false: Q. 16 to 18)
3 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Archive
42 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Numerical Value Type for JEE Main
15 Videos
- SEQUENCE AND SERIES BOOK - VMC MODULES ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - JEE MAIN & Advance ( ARCHIVE)
46 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - JEE ADVANCED (ARCHIVE)
34 Videos
Similar Questions
A straight line through the origin 'O' meets the parallel lines 4x+2y=9 and 2x+y=−6 at points P and Q respectively. Then the point 'O' divides the segment PQ in the ratio
View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionA straight line through the point A (−2,−3) cuts the line x+3y=9 and x+y+1=0 at B and C respectively. If AB.AC=20 then equation of the possible line is
View SolutionThe tangent drawn to the hyperbola x216−y29=1, at point P in the first quadrant whose abscissa is 5, meets the lines 3x−4y=0and3x+4y=0 at Q and R respectively. If O is the origin, then the area of triangle OQR is (in square units)
View SolutionThe line xa+yb=1 meets the axis of and y at A and B respectively and C is middle point of AB then
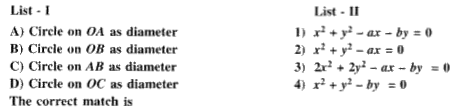
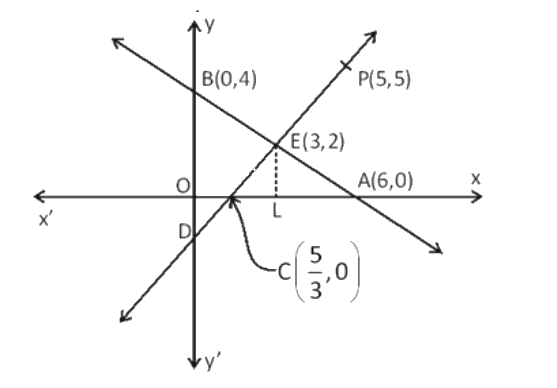
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionFind the point of intersection of the lines 2x−3y+8=0 and 4x+5y=6
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View SolutionThe line y=3x4 meets the lines x−y+1=0 and 2x−y=5 at A and B respectively. Coordinates of P on y=3x4 such that PA⋅PB=25.
View Solution
