If p,q,r have truth values T,F,T respectively, which of the following is true ?
The correct Answer is:D
To determine which of the given statements is true based on the truth values of p, q, and r (where p=T, q=F, and r=T), we will evaluate each option step by step.
Step 1: Evaluate P⟹Q and R
1. Identify the values:
- p=T
- q=F
- r=T
2. Evaluate P⟹Q:
- The implication P⟹Q is only false when p is true and q is false.
- Here, T⟹F is false.
3. Combine with R:
- Now we have (P⟹Q)∧R.
- This becomes F∧T.
- Since false and true is false, the result is false.
Step 2: Evaluate P⟹Q and ¬R
1. Evaluate ¬R:
- Since r=T, ¬R=F.
2. Combine:
- We have (P⟹Q)∧¬R.
- This becomes F∧F.
- The result is false.
Step 3: Evaluate Q⟹P and R
1. Evaluate Q⟹P:
- Here, q=F and p=T.
- The implication Q⟹P is true because false implies true is true.
2. Combine with R:
- We have (Q⟹P)∧R.
- This becomes T∧T.
- The result is true.
Step 4: Evaluate P∧Q and P∨R
1. Evaluate P∧Q:
- Here, p=T and q=F.
- The conjunction P∧Q is T∧F, which is false.
2. Evaluate P∨R:
- Here, p=T and r=T.
- The disjunction P∨R is T∨T, which is true.
3. Combine:
- We have (P∧Q)∨(P∨R).
- This becomes F∨T, which is true.
Conclusion
After evaluating all options, we find that:
- Option 1: False
- Option 2: False
- Option 3: False
- Option 4: True
Thus, the correct answer is Option 4.
- p=T
- q=F
- r=T
- The implication P⟹Q is only false when p is true and q is false.
- Here, T⟹F is false.
- Now we have (P⟹Q)∧R.
- This becomes F∧T.
- Since false and true is false, the result is false.
- Since r=T, ¬R=F.
- We have (P⟹Q)∧¬R.
- This becomes F∧F.
- The result is false.
- Here, q=F and p=T.
- The implication Q⟹P is true because false implies true is true.
- We have (Q⟹P)∧R.
- This becomes T∧T.
- The result is true.
- Here, p=T and q=F.
- The conjunction P∧Q is T∧F, which is false.
- Here, p=T and r=T.
- The disjunction P∨R is T∨T, which is true.
- We have (P∧Q)∨(P∨R).
- This becomes F∨T, which is true.
- Option 2: False
- Option 3: False
- Option 4: True
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test
20 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Section II - Assertion Reason Type
3 Videos
- MATHEMATICAL INDUCTION BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise
30 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
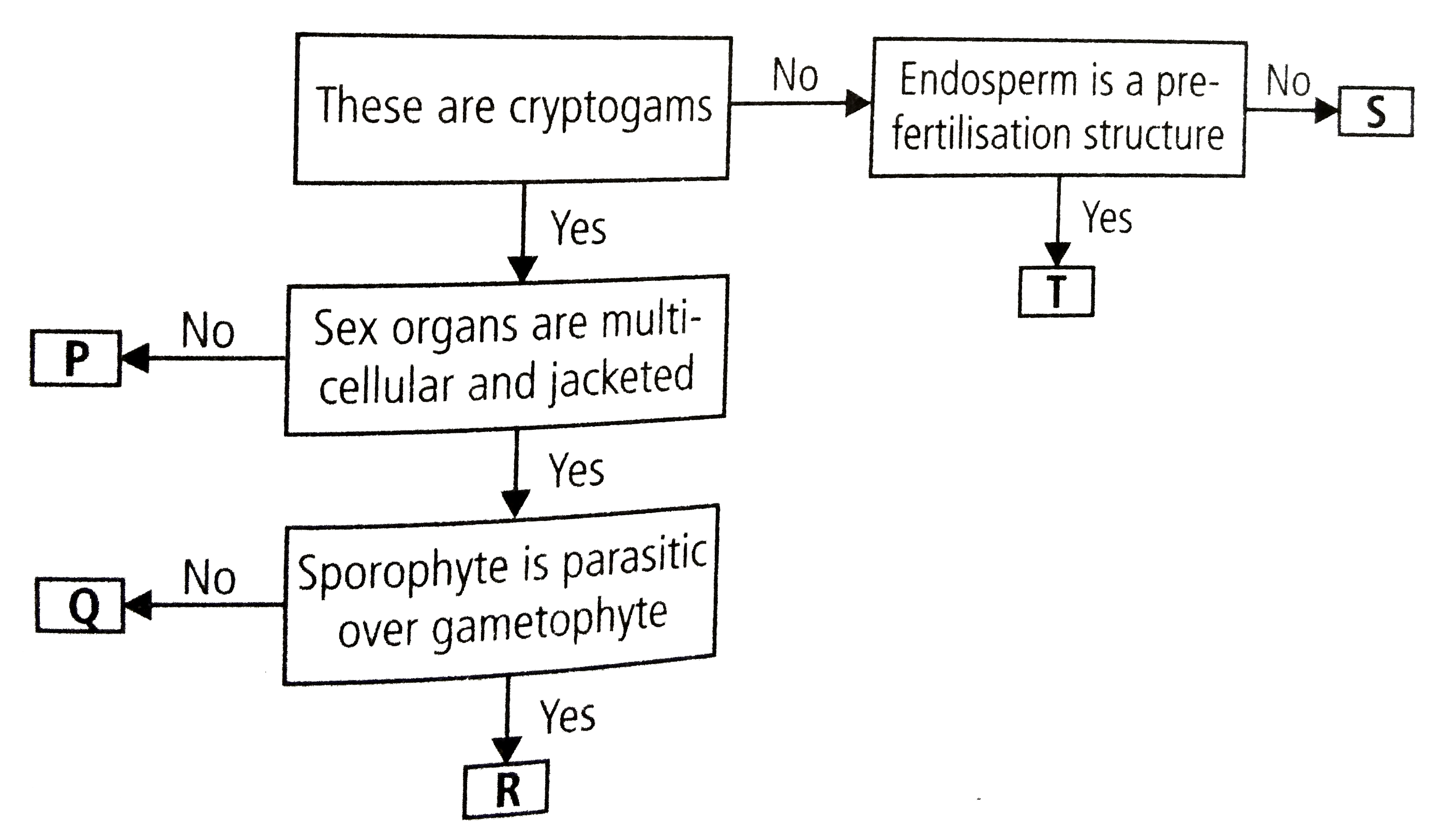
Refer to the given flow chart regarding different groups of kingdom plantae.
Which of the following is true regarding P,Q,R,S and T?AExamples of group 'P' include Riccia, Marchantia, Sphagnum, etc.BMembers of group 'R' can be both homosprous as well as heterosporous.CGroup 'Q' includes seedless vascular plants having sprophytic plant body.DGroup 'S' is more ancient that group 'T' and formed a dominant vegetation on earth some 200 million years back in mesozoic era.For all t>0,f(x)=t2−1t−1−t . Which of the following is true about f(t) ?
AIt increases in proportion to t.BIt increases in proportion to t2.CIt decreases in proportion to t.DIt remains constant .
If each of the statements p→~q,~r→q and p are true then which of the following is NOT true ?
View SolutionThe incorrect statement is
(A) p →q is logically equivalent to ~p ∨ q.
(B) If the truth-values of p, q r are T, F, T respectively, then the truth value of (p ∨ q) ∧ (q ∨ r) is T.
(C) ~(p ∨ q ∨ r) = ~p ∧ ~q ∧ ~r
(D) The truth-value of p ~ (p ∧ q) is always T
View SolutionIf p,q and r are simple propositions with truth values T,F and T , respectively, then the truth value of (~p∨q)∧~r→p is
View SolutionThe incorrect statement is (a) p→−q is logically equivalent to ~p∨q. (b) If the truth-values ofp,q,r are T,F,T respectively, then the truth value of (p∨q)∧(q∨r) is T. (c) ~(p∨q∨r)≡~p∧~q∧~r (d) The truth value of p∧~(p∧q) is always T.
View SolutionGiven that P+Q+R=0. Which of the following statement is true?
View SolutionIf p,q and r are simple propositions with truth values T,F,T then what is the truth value of [(~p∨q) ^−q]→p.
View Solution
