If the area(!) and an angle(θ) of a triangle are given , when the side opposite to the given angle is minimum , then the length of the remaining two sides are
√2!sinθ,√3!sinθ
√2!sinθ,√2!sinθ
√4!sinθ,√4!sinθ
√6!sinθ,√6!sinθ
To solve the problem, we need to find the lengths of the remaining two sides of a triangle when the area and an angle (θ) are given, and the side opposite to the given angle is minimized.
1. Understanding the Triangle:
Let triangle ABC have sides A, B, and C, where C is the side opposite to angle θ. We are given the area of the triangle and the angle θ.
2. Area of the Triangle:
The area (Δ) of triangle ABC can be expressed using the formula:
Δ=12×A×B×sin(θ)
Rearranging this gives:
A×B=2Δsin(θ)
3. Using the Law of Cosines:
According to the Law of Cosines, we have:
C2=A2+B2−2ABcos(θ)
4. Minimizing Side C:
To minimize side C, we can express C in terms of A and B. Substituting A×B from the area equation into the Law of Cosines gives:
C2=A2+B2−2Δcos(θ)sin(θ)
5. Finding the Relationship:
To find the lengths of sides A and B when C is minimized, we can set A=k and B=2Δksin(θ) for some constant k. This leads to:
C2=k2+(2Δksin(θ))2−2k⋅2Δksin(θ)cos(θ)
6. Setting Up for Minimum C:
To minimize C, we can differentiate with respect to k and set the derivative to zero. This will give us the optimal lengths of A and B.
7. Conclusion:
The minimum lengths of sides A and B occur when they are equal, leading to:
A=B=√2Δsin(θ)
Thus, the lengths of the remaining two sides are equal and can be expressed in terms of the area and the angle.
Final Answer:
The lengths of the remaining two sides A and B are:
A=B=√2Δsin(θ)
Let triangle ABC have sides A, B, and C, where C is the side opposite to angle θ. We are given the area of the triangle and the angle θ.
The area (Δ) of triangle ABC can be expressed using the formula:
Δ=12×A×B×sin(θ)
Rearranging this gives:
A×B=2Δsin(θ)
According to the Law of Cosines, we have:
C2=A2+B2−2ABcos(θ)
To minimize side C, we can express C in terms of A and B. Substituting A×B from the area equation into the Law of Cosines gives:
C2=A2+B2−2Δcos(θ)sin(θ)
To find the lengths of sides A and B when C is minimized, we can set A=k and B=2Δksin(θ) for some constant k. This leads to:
C2=k2+(2Δksin(θ))2−2k⋅2Δksin(θ)cos(θ)
To minimize C, we can differentiate with respect to k and set the derivative to zero. This will give us the optimal lengths of A and B.
The minimum lengths of sides A and B occur when they are equal, leading to:
A=B=√2Δsin(θ)
Thus, the lengths of the remaining two sides are equal and can be expressed in terms of the area and the angle.
The lengths of the remaining two sides A and B are:
A=B=√2Δsin(θ)
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
If area of ΔABC(Δ) and angle C are given and if c opposite to given angle is minimum, then
View SolutionIn a triangle the greater angle has the longer side opposite to it.
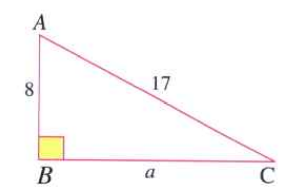
View SolutionFind the length of side BC in the given triangle.
View SolutionLet Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf the length of sides of right angled triangle are in AP, then their ratio is
View SolutionThe sides of a right angled triangle are in arithmetic progression. If the triangle has area 24, then what is the length of its smallest side?
View SolutionThe sides of the right angled triangle are in arithmetic progression. If the triangle has area 24, then what is the length of its smallest side ?
View Solution
