If in a ,CD is the bisector of then CD =
To find the length of the angle bisector CD in triangle ABC where CD bisects ∠ACB, we can use the Angle Bisector Theorem and some properties of triangles. Here’s the step-by-step solution:
Step 1: Understand the Angle Bisector Theorem
The Angle Bisector Theorem states that the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the lengths of the other two sides of the triangle. In triangle ABC, if CD is the bisector of ∠ACB, then:
ADDB=ACBC
Let AC=b and BC=a.
Step 2: Assign Variables
Let AD=x and DB=y. According to the theorem:
xy=ba
This implies:
x=bay
Step 3: Express Total Length
The total length AB can be expressed as:
AB=AD+DB=x+y
Substituting x from the previous step:
AB=bay+y=y(ba+1)=y(b+aa)
Thus:
y=AB⋅ab+a
And substituting back for x:
x=bay=ba⋅AB⋅ab+a=AB⋅bb+a
Step 4: Use the Length of the Angle Bisector Formula
The length of the angle bisector CD can be calculated using the formula:
CD=2⋅AB⋅AC⋅BC(AC+BC)2⋅cos(C2)
Substituting AC=b and BC=a:
CD=2⋅AB⋅a⋅b(a+b)2⋅cos(C2)
Final Expression
Thus, the length of the angle bisector CD is given by:
CD=2aba+b⋅cos(C2)
The Angle Bisector Theorem states that the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the lengths of the other two sides of the triangle. In triangle ABC, if CD is the bisector of ∠ACB, then:
ADDB=ACBC
Let AC=b and BC=a.
Let AD=x and DB=y. According to the theorem:
xy=ba
This implies:
x=bay
The total length AB can be expressed as:
AB=AD+DB=x+y
Substituting x from the previous step:
AB=bay+y=y(ba+1)=y(b+aa)
Thus:
y=AB⋅ab+a
And substituting back for x:
x=bay=ba⋅AB⋅ab+a=AB⋅bb+a
The length of the angle bisector CD can be calculated using the formula:
CD=2⋅AB⋅AC⋅BC(AC+BC)2⋅cos(C2)
Substituting AC=b and BC=a:
CD=2⋅AB⋅a⋅b(a+b)2⋅cos(C2)
Thus, the length of the angle bisector CD is given by:
CD=2aba+b⋅cos(C2)
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
In a triangle ABC,CD is the bisector of the angle C. If cos(C2) has the value 13andl(CD)=6, then (1a+1b) has the value equal to -
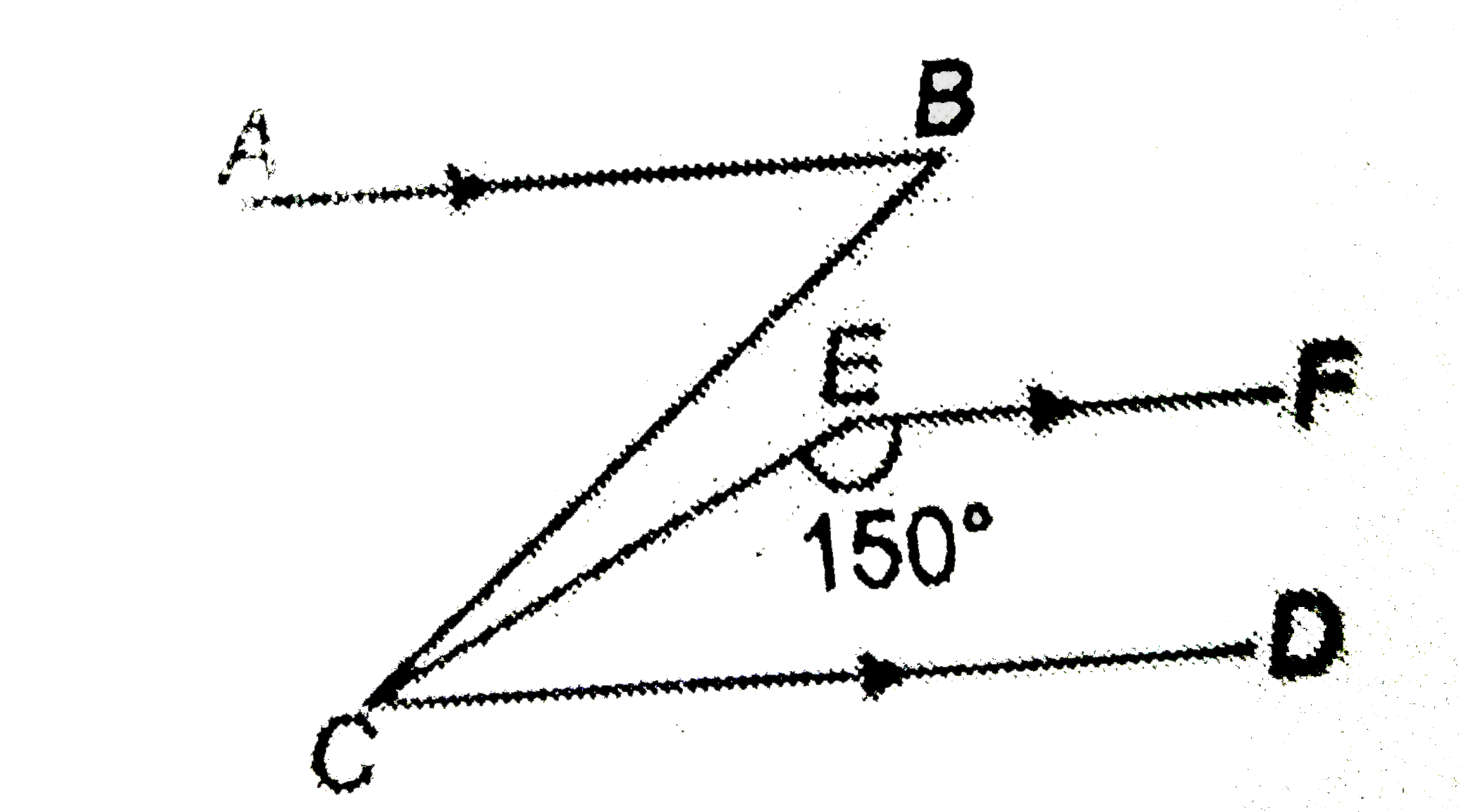
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
View SolutionIn a quadrilateral ABCD, AC is the bisector of the (AB, AD) which is 2π3, 15|AC|=3|AB|=5|AD|, then cos(BA,CD) is equal to
View SolutionIn TriangleABC with fixed length of BC, the internal bisector of angle C meets the side ABatD and the circumcircle at E . The maximum value of CD×DE is c2 (b) c22 (c) c24 (d) none of these
View SolutionIn a triangle ABC, D is a point on BC such that AD is the internal bisector of ∠A. Let ∠B=2∠C and CD = AB. Then ∠A is
View SolutionIn triangle ABC,∠C=2π3andCD is the internal angle bisector of ∠C meeting the side AB at D. If Length CD is 1, then H.M. of aandb is equal to : (a) 1 (b) 2 (c) 3 (d) 4
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
E is equidistant from A and B
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
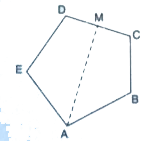
View SolutionABCDE is a regular pentagon. The bisector of angle A of the pentagon meet the side CD in point M. Show that ∠AMC=90∘.
View SolutionABCD is a quadrilateral in which AB=AD . The bisector of BAC and CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF||BD.
View Solution
