If the perimeter of a triangle and the diameter of an ex-circle are equal , then the triangle is
right angled isosceles
right angled
equilateral
isosceles
Let ABC be the triangle such that
a+b+c=2r1
⇒2R(sinA+sinB+sinC)=8RsinA2cosB2cosC2
⇒2R×4cosA2cosB2cosC2=8RsinA2cosB2cosC2
⇒cosB2cosC2(cosA2−sinA2)=0
⇒cosA2−sinA2=0⇒tanA2=1⇒A=π2
Hence, the triangle ABC is right angled at A.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
Find the perimeter of each triangle.
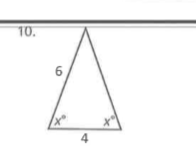
View SolutionFind the perimeter of each triangle.
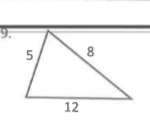
View SolutionIf the perimeter of a triangle is 6, then its maximum area is
View SolutionLet a and b represent the lengths of a right triangles legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle circumscribed on the triangle, the d+D equals. (a)a+b (b) 2(a+b) (c)12(a+b) (d) √a2+b2
View SolutionThere is an equilateral triangle with side 4 and a circle with the centre on one of the vertex of that triangle. The arc of that circle divides the triangle into two parts of equal area. How long is the radius of the circle?
View SolutionIn an isosceles triangle, each of the two equal sides is 10cm less than three times the base. If the perimeter of the triangle is 330cm, find the lengths of the sides of the triangle.
View SolutionThe lengths of the sides of a triangle are in the ratio 2:3:4. If the perimeter of the triangle is 63 cm, find the lengths of the sides of the triangle.
View SolutionProve that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
View SolutionIn the given figure, OP is equal to the diameter of the circle. Prove that △ABP is an equilateral triangle.
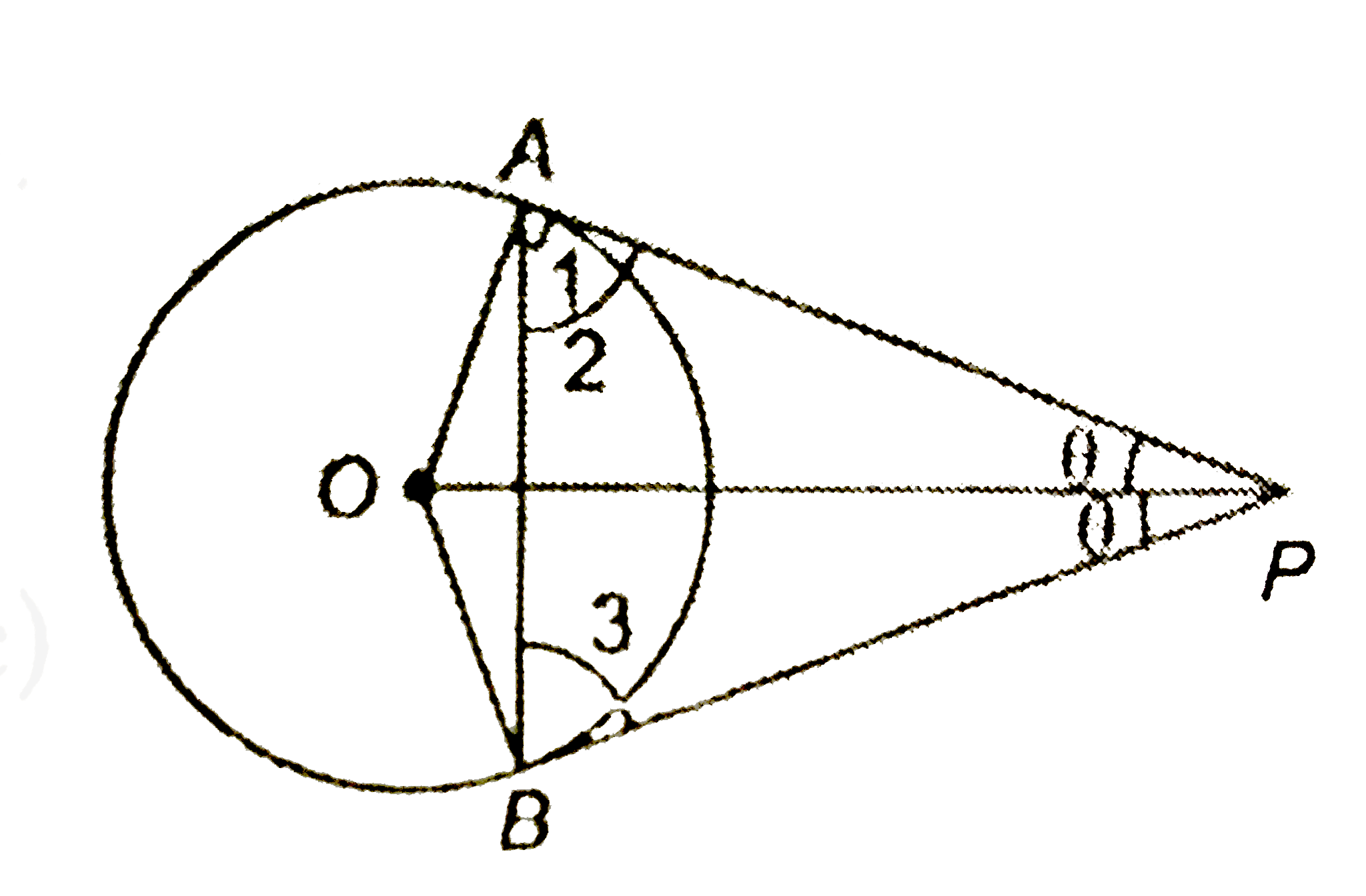
View SolutionIf the perimeter of the triangle formed by feet of altitudes of the triangle ABC is equal to four times the circumradius of ΔABC, then identify the type of ΔABC
View Solution
