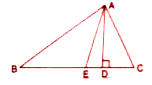
ABC is a triangle. D is the middle point of BC. If AD is perpendicular to AC, The value of cos A cos C , is
(3c2−a2ac
a2−c22ac
(2c2−a23ac
none of these
To solve the problem, we need to find the value of cosAcosC given that D is the midpoint of BC and AD is perpendicular to AC.
1. Draw Triangle ABC:
- Let A, B, and C be the vertices of the triangle.
- Let D be the midpoint of side BC.
2. Label the Sides:
- Let AB=c, AC=b, and BC=a.
- Since D is the midpoint of BC, we have BD=DC=a2.
3. Use the Given Condition:
- Since AD is perpendicular to AC, we can use trigonometric relationships in triangle ADC.
4. Find cosC:
- In triangle ADC, we can express cosC as:
cosC=ADAC=ADb
- By the definition of cosine in triangle ADC, we can also use the cosine rule:
cosC=b2+(a2)2−c22b⋅a2=b2+a24−c2ab
5. Find cosA:
- Similarly, we can express cosA in triangle ABD:
cosA=ADAB=ADc
- Using the cosine rule in triangle ABD:
cosA=c2+(a2)2−b22c⋅a2=c2+a24−b2ac
6. Calculate cosAcosC:
- Now we multiply cosA and cosC:
cosAcosC=⎛⎜⎝c2+a24−b2ac⎞⎟⎠⎛⎜⎝b2+a24−c2ab⎞⎟⎠
7. Simplify the Expression:
- After simplification, we will find that:
cosAcosC=2(c2−b2)3ab
8. Final Result:
- Therefore, the value of cosAcosC is:
cosAcosC=2(c2−b2)3ab
Conclusion:
The correct option from the given choices is option 3, which states:
cosAcosC=2(c2−b2)3ab
- Let A, B, and C be the vertices of the triangle.
- Let D be the midpoint of side BC.
- Let AB=c, AC=b, and BC=a.
- Since D is the midpoint of BC, we have BD=DC=a2.
- Since AD is perpendicular to AC, we can use trigonometric relationships in triangle ADC.
- In triangle ADC, we can express cosC as:
cosC=ADAC=ADb
- By the definition of cosine in triangle ADC, we can also use the cosine rule:
cosC=b2+(a2)2−c22b⋅a2=b2+a24−c2ab
- Similarly, we can express cosA in triangle ABD:
cosA=ADAB=ADc
- Using the cosine rule in triangle ABD:
cosA=c2+(a2)2−b22c⋅a2=c2+a24−b2ac
- Now we multiply cosA and cosC:
cosAcosC=⎛⎜⎝c2+a24−b2ac⎞⎟⎠⎛⎜⎝b2+a24−c2ab⎞⎟⎠
- After simplification, we will find that:
cosAcosC=2(c2−b2)3ab
- Therefore, the value of cosAcosC is:
cosAcosC=2(c2−b2)3ab
The correct option from the given choices is option 3, which states:
cosAcosC=2(c2−b2)3ab
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
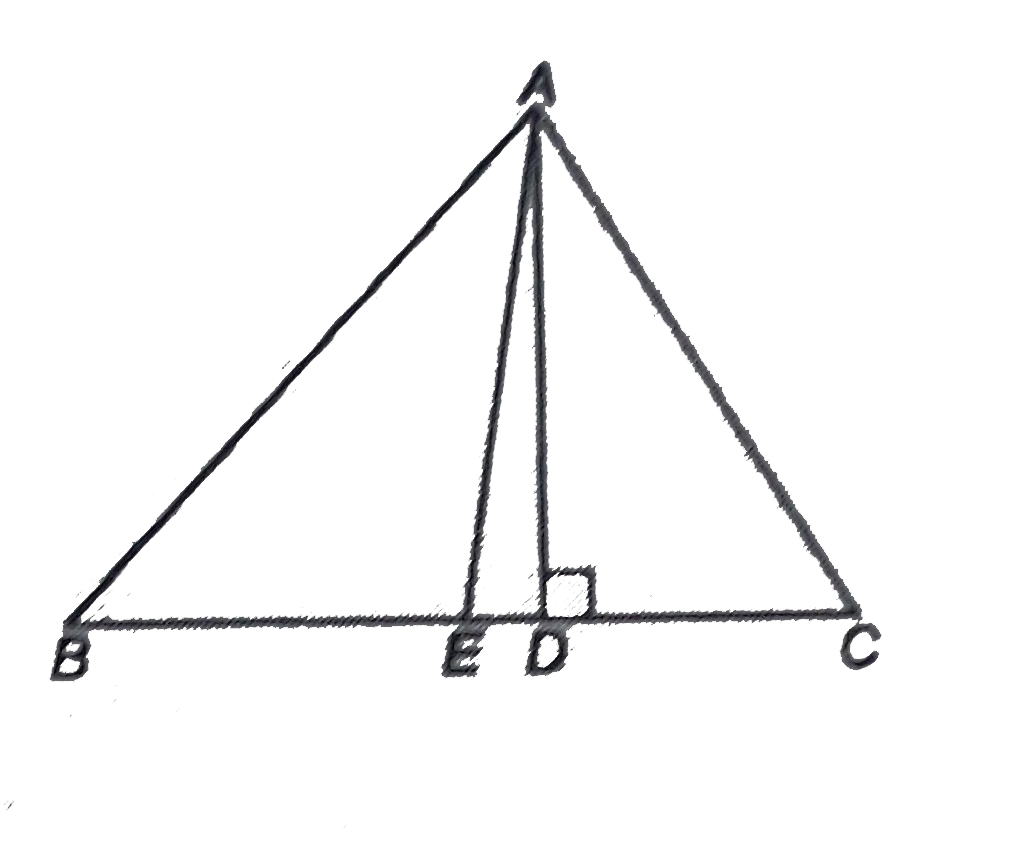
In triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that : AB2+AC2=2AE2+2BE2
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
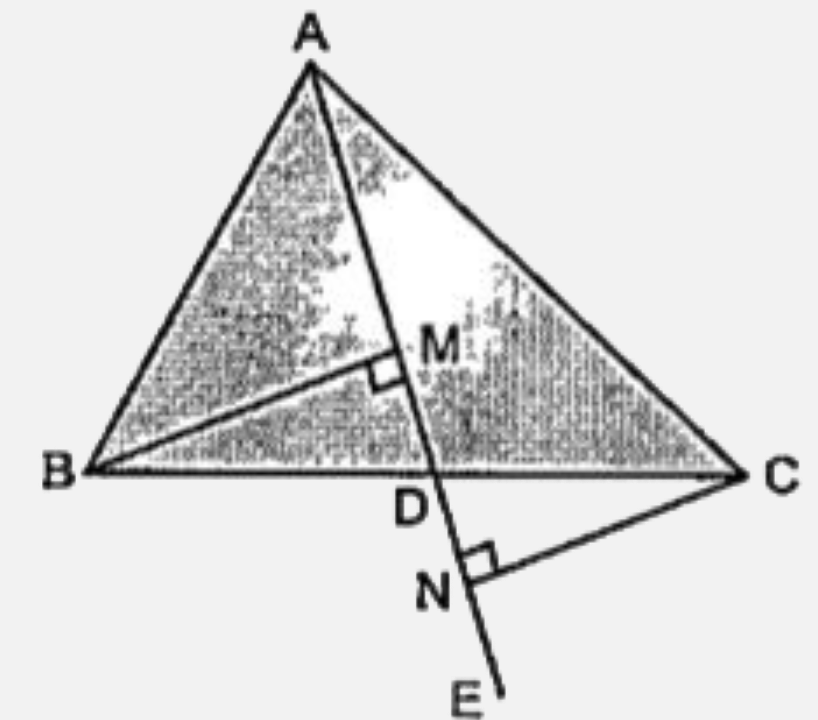
Prove that :
BM=CN
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.

Prove that :
ΔBMD≅ΔCND
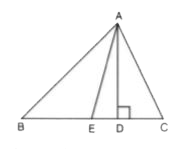
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

ΔADE~ΔACB.
View SolutionIn a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
View Solution
