If in a !ABC,∠A=π/3 and AD is a median , then
2AD2=b2+c2+bc
4AD2=b2+c2+bc
6AD2=b2+c2+bc
none of these
The correct Answer is:B
Step by step video solution for If in a !ABC,angleA=pi//3 and AD is a median , then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
If in a △ABC,A=π3andAD is the median, then
View SolutionIn △ABC,∠A=π3andb:c=2:3,tanθ=√35,0<θ<π2 then
View SolutionIn triangle ABC medians AD and CE are drawn, if AD=5, ∠DAC=π8 and ∠ACE=π4, then the area of triangle ABC is equal to a. 258 b. 253 c. 2518 d. 103
View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionIf A(4,−6),B(3,−2)andC(5,2) are the vertices of A B C, and AD is median then verify the fact that a median of a triangle ABC divides it into two triangles of equal areas.
View SolutionIf A(4,−6),B(3,−2)andC(5,2) are the vertices of a ΔABCandAD is its median, prove that the median AD divides ΔABC into two triangles of equal areas.
View SolutionIn a triangle ABC, medians ADandCE are drawn. If AD=5,∠DAC=π8and∠ACE=π4then the area of the triangle ABC is equal to 5ab, then a+b is equal to
View SolutionIn a triangle ABC, AD is a medium and E is mid-point of median AD. A line through B and E meets AC at point F.
View SolutionIn a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point E. Prove that : AC = 3AF Draw DG parallel to BF, which meets AC at point G.
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
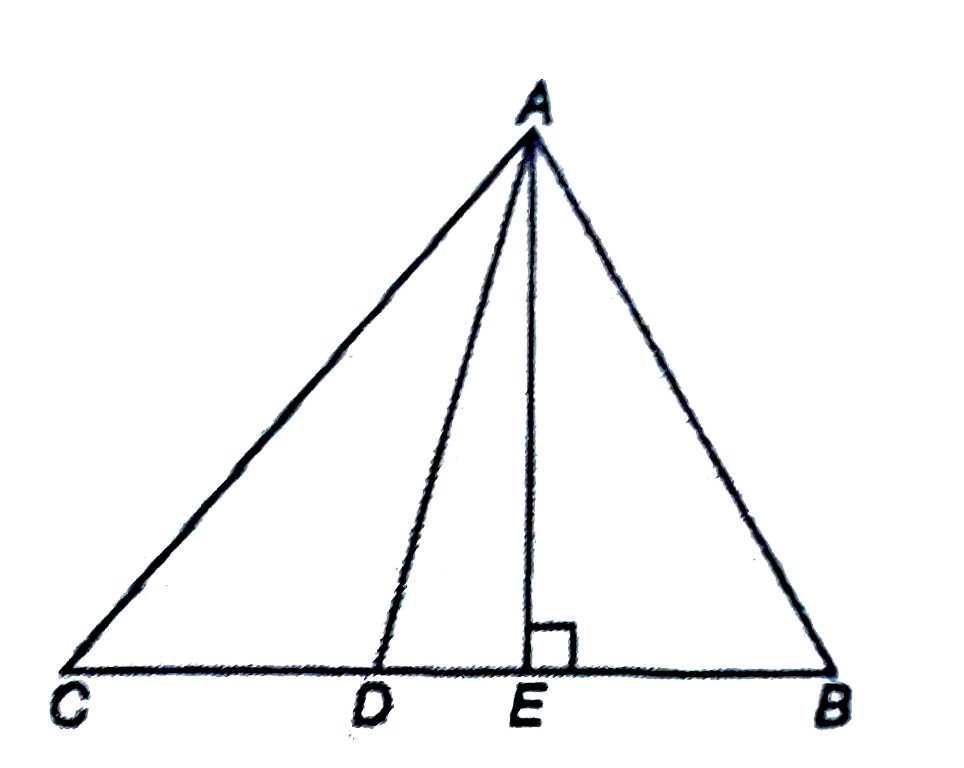
View Solution
