If AD, BE and CF are the medians of a ΔABC, then evaluate (AD2+BE2+CF2):(BC2+CA2+AB2).
4:3
3:2
3:4
2:3
The correct Answer is:C
Step by step video & image solution for If AD, BE and CF are the medians of a Delta ABC, then evaluate (AD^(2)+BE^(2)+CF^(2)): (BC^(2) +CA^(2) +AB^(2)). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
If AD,BEandCF are the medians of a ΔABC,then(AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionIf AD,BEandCF be the median of a △ABC, prove that −−→AD+−−→BE+−−→CF=0
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionIf G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionAD, BE and CF asre the medians of a triangle ASBC intersectiing in G. Show that △AGB=△BGC=△CGA=13△ABC.
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
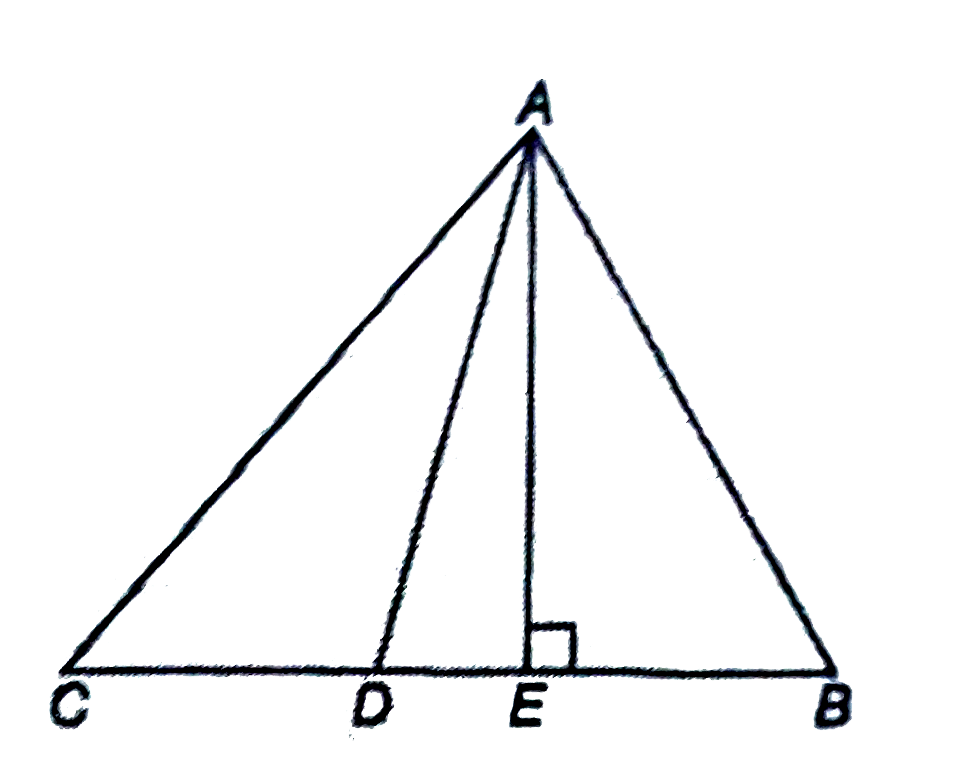
View SolutionLet AD be a median of the ΔABC. If AE and AF are medians of the triangle ABD and ADC, respectively, and BD=a/2 AD = m1,AE=m2,AF=m3, then a2/8 is equal to
View SolutionIf AD, BE and CF are the altitudes of ΔABC whose vertex A is (-4,5). The coordinates of points E and F are (4,1) and (-1,-4), respectively. Equation of BC is
View Solution