Given below is a magic square. Place the numbers 7095,−21−133,2595,2438 in the appropriate squares so that sum in each row, column and diagonal is equal.
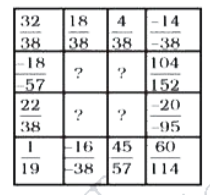
Hint: (Rewrite each rational number in its lowest term.)
Step by step video & image solution for Given below is a magic square. Place the numbers (70)/(95), (-21)/(-133), (25)/(95), (24)/(38) in the appropriate squares so that sum in each row, column and diagonal is equal. Hint: (Rewrite each rational number in its lowest term.) by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Think and Discuss
1 Videos
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Exercise
84 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Think and Discuss
1 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
Similar Questions
In a “magic square”, the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square?

View SolutionIn a magic square, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
View SolutionIn a “magic square”, the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square? TABLE
View SolutionIn a magic square each row, column and diagonal have the same sum , then the values of A and B are
View SolutionIn a magic square each row, column and diagonal have the same sum. Check which of the following is a magic square.
View SolutionIn a magic square, each row.column and diagonal have the same sum. Check which of the following is a magic square.
View SolutionComplete the magic square given below, so that the sum of the number in each row or in each column or along each diagonal is 15
View SolutionLet A=[aij]3×3 be a matrix whose elements are distinct integers from 1,2,3,...,9. The matrix is formed so that the sum of the numbers is every row, column and each diagonal is a multiple of 9. If number of all such possible matrices is lambda, then lambda is divisible by
View SolutionFill in the blank space of the following magic square so that the sum of the numbers in each row, each column and each of the diagonals is – 6.
(i)
In this magic square, sum of the numbers in every row, column and each of the diagonals is – 2. Fill in the blank:

View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
View Solution
