Two different conductors have same resistances at 0∘C. It is found that the resistances of the first conductor at t∘1C is equal to the resistances of the second conductor at t∘2C, The ratio of the temperature coefficients of resistances of the conductors a1a2 is
A
t1t2
B
t2−t1t2
C
t2−t1t1
D
t2t1
Text Solution
The correct Answer is:D
Resistance of a conductor varies linearly with temperature as
Rt=R0(1+at)
for first conductor
Rt=R0(1+a1t2)
or a1=Rt1−R0t1……(i)
Similarly for second conductor
a2=Rt2−R0t2…..(ii)
From Eqs. (i) and (ii) we get,
a1a2=t2t
|
Similar Questions
Knowledge Check
Two different conductors have same resistance at 0∘ C It is found that the resistance of the first conductor at t∘1 C is equal to the resistance of the second conductor at t∘2 C. The ratio of temperature coefficients of resistance of the conductors,a1a2 is
At1t2Bt2−t1t2Ct2−t1t1Dt2t1The temperature coefficient of resistance of a conductor is
APositive alwaysBNegative alwaysCzeroDInfiniteThe temperature coefficient of resistance of a semi conductor is
AIs always positiveBIs always negativeCIs zeroDMay be positive or negative or zero
The ratio of the resistances of a conductor at a temperature of 15∘C to its resistance at a temperature of 37.5∘C is 4:5. The temperature coefficient of resistance of the conductor is
View SolutionVariation of resistance of the conductor with temperature is shown . Temperature coefficient of the conductor is
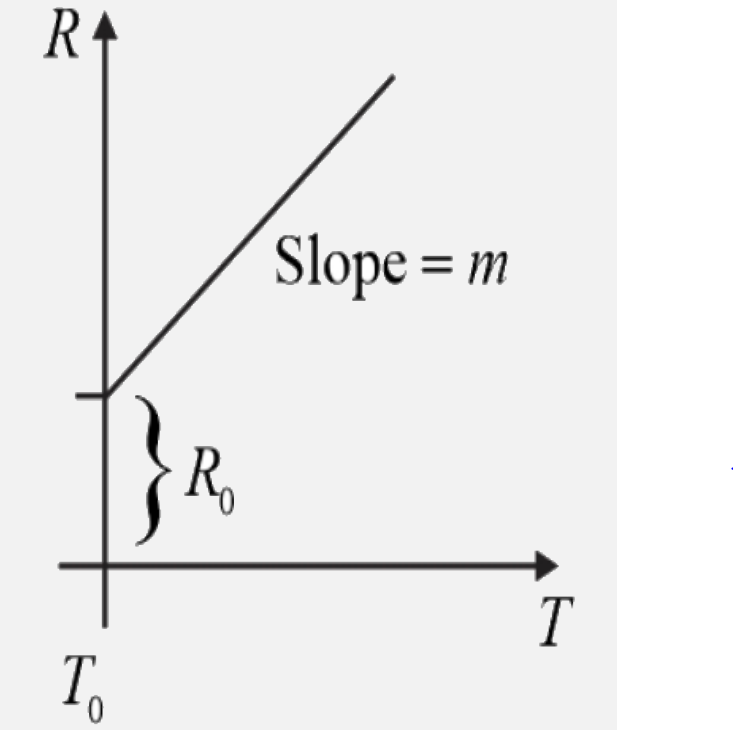
View SolutionVariation of resistance of the conductor with temperature is shown . Temperature coefficient of the conductor is

View SolutionThe ratio of the resistances of a conductor at a temperature of 15∘C to its resistance at a temperature of 37.5∘C is 4:5. The temperature coefficient of resistance of the conductor is
View SolutionAs the temperature increases, resistivity of semi-conductor:
View Solution
