The time period of revolution of a charge q1 and of mass m moving in a circular path of radius r due to Coulomb force of attraction with another charge q2 at its centre isSolution in Malayalam
√16πε0mr3q1q2
√8π2ε0mr3q1q2
√ε0mr316q1q2
√16π3ε0mr3q1q2
The correct Answer is:D
Centripetal force F=mv2r ...(i)
and electrostatic force
F=K.q1.q2r2 ...(ii)
Equating both equation
mv2r=K.q1q2r2
v=√km.q1q2r
The time period of revolution
T=2πrv
=2πr√m.rk.q1q2
=√4π2r2mrK.q1q2 (∵K=14πε0)
T=√4π2r2mr.4πε0q1q2
=√16π2ε0mr3q1q2
Similar Questions
The time period of revolution of a charge q1 and of mass m moving in a circular path of radius due to Coulomb force of attraction with another charge q2, at its centre is
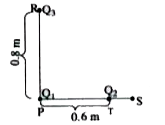
View SolutionTwo charges Q1andQ2 Coulombs are shown in fig. A third charge Q3 coulomb is moved from point R to S along a circular path with P as centre Change in potential energy is
View SolutionCharge q2 of mass m revolves around a stationary charge q1 in a circulare orbit of radius r. The orbital periodic time of q2 would be
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionCharge q2 is at the centre of a circular path with radius r. work done in carrying charge q1 once around this equipotential path , would be
View SolutionA particle of mass m carrying charge '+q_(1)' is revolving around a fixed charge '-q_(2)' in a circular path of radius r. Calculate the period of revolution.
View SolutionCharge q_(1) is at the centre of a circular path with radius a Work done in carrying charge q_(1) , once around this apportional path, would be
View Solution
