Charge q2 is at the centre of a circular path with radius r. work done in carrying charge q1 once around this equipotential path , would be
14πε0×q1q2r2
14πε0×q1q2r
zero
Infinity
The correct Answer is:C
To solve the problem of finding the work done in carrying charge q1 once around an equipotential path where charge q2 is at the center, we can follow these steps:
1. Understanding Equipotential Surfaces:
- An equipotential surface is defined as a surface where the electric potential is constant throughout. This means that no work is done when moving a charge along this surface.
2. Identifying the Charges:
- We have two charges: q1 (the charge being moved) and q2 (the charge at the center of the circular path).
3. Analyzing the Work Done:
- The work done W in moving a charge in an electric field is given by the formula:
W=q⋅ΔV
where q is the charge being moved and ΔV is the change in electric potential.
4. Determining the Change in Potential:
- Since the path is an equipotential path, the potential difference ΔV when moving from one point to another on this path is zero:
ΔV=Vfinal−Vinitial=0
5. Calculating the Work Done:
- Substituting ΔV=0 into the work done formula:
W=q1⋅0=0
6. Conclusion:
- Therefore, the work done in carrying charge q1 once around the equipotential path is:
W=0
Final Answer:
The work done in carrying charge q1 once around this equipotential path is 0.
---
- An equipotential surface is defined as a surface where the electric potential is constant throughout. This means that no work is done when moving a charge along this surface.
- We have two charges: q1 (the charge being moved) and q2 (the charge at the center of the circular path).
- The work done W in moving a charge in an electric field is given by the formula:
W=q⋅ΔV
where q is the charge being moved and ΔV is the change in electric potential.
- Since the path is an equipotential path, the potential difference ΔV when moving from one point to another on this path is zero:
ΔV=Vfinal−Vinitial=0
- Substituting ΔV=0 into the work done formula:
W=q1⋅0=0
- Therefore, the work done in carrying charge q1 once around the equipotential path is:
W=0
The work done in carrying charge q1 once around this equipotential path is 0.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - B
38 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Knowledge Check
The work done to move a unit charge along an equipotential from P to Q
Amust be defined as −Q∫P→E.→dlBis zeroCcan have a non-zero valueDboth (a) and (b)are correctThe work done in carrying a charge q once round a circle of radius r with a charge Q at the centre is
AqQ4πε0aBqQ4πε0a2Cq4πε0aDzero
A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R > r). The potential difference between the two is
View SolutionThe work done to move a charge along an equipotential from A to B
View SolutionThe work done to move a charge along an equipotential from A to B
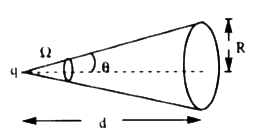
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
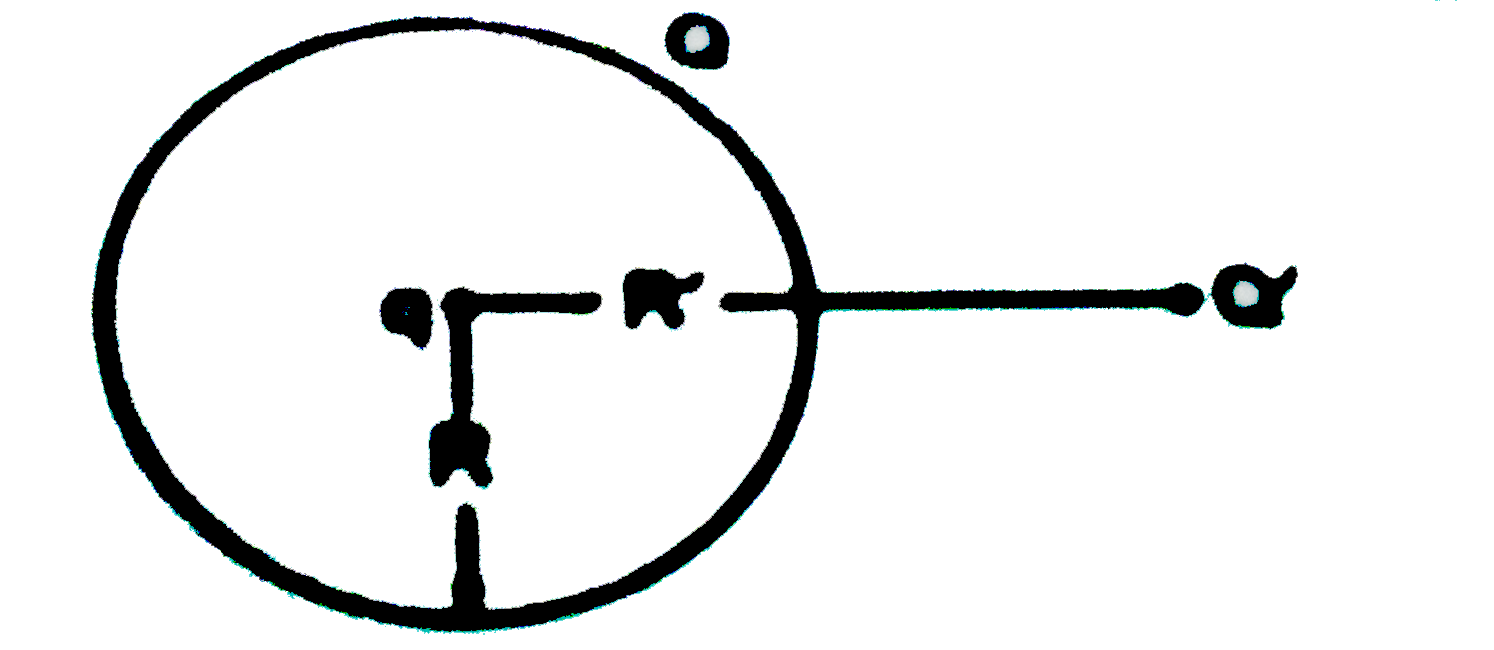
View SolutionA charge 'q' is placed at the centre of a conducting spherical shell of radius R, which is given a charge Q. An external charge Q' is also present at distance R'(R'>R) from 'q'. Then the resultant field will be best represented for region r<R by : [where r is the distance of the point from q]
View SolutionWhen an electron moves in a circular path around a stationary nucleus charge at the center
View Solution
