From the ground, a projectile is fired at an angle of 60 degrees to the horizontal with a speed of 20 m/s. Take, acceleration due to gravity as 10 ms2 . The horizontal range of the projectile is
10√3m
20 m
20√3m
40√3m
The correct Answer is:C
The horizontal range
R=(u2sin2θ)/(g)
=20×2010×√132=20√3m
Similar Questions
From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
View SolutionA particle is projected at an angle of60∘ above the horizontal with a speed of 10m/s .When the projectile reaches highest point, change in velocity is
View Solution
Knowledge Check
From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
A10√3B20 mC20√3mD40√3A projectile is fired horizontally with an initial speed of 20 m/s/ its horzontal speed 3 sec later is:
A20m/sB6.67m/sC60m/sD29.4m/sA projectile is projected at a angle 60∘ with horozontal with speed 10 m/s. The minimum radius of curvature of the trajectory described by the projectile is
A2.55mB2 mC10 mDNone of these
A projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
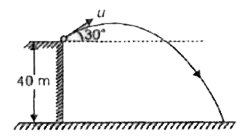
View SolutionFigure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
View SolutionA projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
View SolutionFigure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is

View SolutionA projectile is launched with a speed of an angle 60∘ with the horizontal from a sloping surface of inclination 30∘. The range R is: (g=10m/s2)
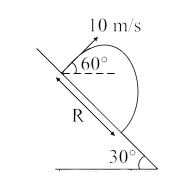
View Solution
