समांतर चतुर्भुज का आधार ज्ञात कीजिए जिसका क्षेत्रफल 560m2 और शीर्षलंब 1400cm है।
The correct Answer is:40 m
दिया गया है :-
समांतर चतुर्भुज का क्षेत्रफल = 560 m2
समांतर चतुर्भुज का शीर्षलंब =1400 cm
मीटर मे बदलने पर :-
∵ 1 m = 100 cm
∴ 1400100=14 मीटर
सूत्र :
समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊंचाई
560 m2 = आधार × 14
आधार =560m214m
आधार =40 मीटर
Topper's Solved these Questions
- परिमाप और क्षेत्रफलBOOK - MBD PUBLICATIONCHAPTER - परिमाप और क्षेत्रफलEXERCISE - पाठ्य-पुस्तक प्रश्नावली 11.3
21 Videos
- परिमाप और क्षेत्रफलBOOK - MBD PUBLICATIONCHAPTER - परिमाप और क्षेत्रफलEXERCISE - पाठ्य-पुस्तक प्रश्नावली 11.3 (अभ्यास के लिए अतिरिक्त प्रश्न)
42 Videos
- परिमाप और क्षेत्रफलBOOK - MBD PUBLICATIONCHAPTER - परिमाप और क्षेत्रफलEXERCISE - पाठ्य-पुस्तक प्रश्नावली 11.2
14 Videos
- त्रिभुजों की सर्वांगसमता BOOK - MBD PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - बहुविकल्पी प्रश्न
6 Videos
- परिमेय संख्याएँ BOOK - MBD PUBLICATIONCHAPTER - परिमेय संख्याएँ EXERCISE - बहुविकल्पी प्रश्न (निम्नलिखित में प्रत्येक प्रश्न के उत्तर के लिए दिए है सही उत्तर का चयन कीजिए)
17 Videos
Similar Questions
निम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए : (π=227) लीजिये
14 cm
View Solution10 cm व्यास वाले एक वृत्त की परिधि ज्ञात कीजिए ? (π=3.14 प्रयोग कीजिए)
View Solutionनिम्न समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
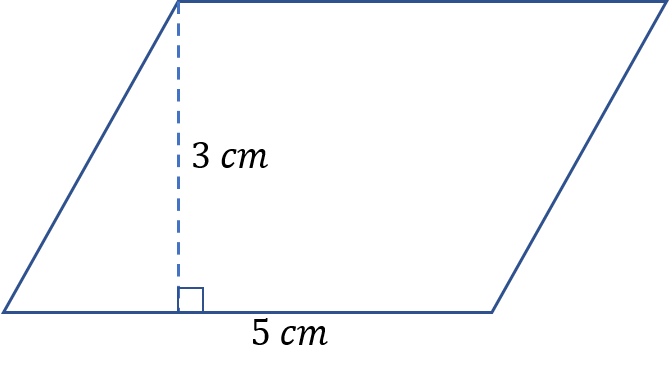
View Solutionनिम्न में से कौन सी वस्तुएँ सर्वांगसम हैं : -
View Solutionनिम्नलिखित में से कौन सी प्राकृत संख्या नहीं है?
View Solutionयदि 9 सेमी ऊँचाई वाले एक लंबवृत्तीय शंकु का आयतन 48π सेमी^(3) गहरा है, तो इसके आधार का व्यास ज्ञात कीजिए ?
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionसदिशों के प्रयोग द्वारा उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(2,3,5),B(3,5,8) और C(2,7,8) हैं |
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसका भुज सदैव 2 रहता है ।
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक रेखा बिंदु 2ˆi+ˆj−3ˆk से गुजरती है और साधीश ˆi+2ˆj+ˆk के समांतर है । रेखा का सदिश समाकरण ज्ञात कीजिए। इसके द्वारा रेखा का कार्तीय समीकरण ज्ञात कीजिए।
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-3,4) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केंद्र (3,2,1) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केन्द्र (2, 2, 1 ) तथा त्रिज्या 4 है।
View Solution
