त्रिभुज का आधार ज्ञात कीजिए जिसका शीर्षलंब 12 cm और क्षेत्रफल 96 cm2 है।
The correct Answer is:16 cm
दिया गया है :-
त्रिभुज का शीर्षलंब =12 cm
त्रिभुज का क्षेत्रफल =96 cm2
ज्ञात करना है :- त्रिभुज का आधार =?
त्रिभुज का क्षेत्रफल =12 (आधार × ऊंचाई )
" "96=1/(cancel2)xx (आधार × cancel12)
96= (आधार × 6)
आधार =966=16 cm
Topper's Solved these Questions
- परिमाप और क्षेत्रफलBOOK - MBD PUBLICATIONCHAPTER - परिमाप और क्षेत्रफलEXERCISE - पाठ्य-पुस्तक प्रश्नावली 11.3
21 Videos
- परिमाप और क्षेत्रफलBOOK - MBD PUBLICATIONCHAPTER - परिमाप और क्षेत्रफलEXERCISE - पाठ्य-पुस्तक प्रश्नावली 11.3 (अभ्यास के लिए अतिरिक्त प्रश्न)
42 Videos
- परिमाप और क्षेत्रफलBOOK - MBD PUBLICATIONCHAPTER - परिमाप और क्षेत्रफलEXERCISE - पाठ्य-पुस्तक प्रश्नावली 11.2
14 Videos
- त्रिभुजों की सर्वांगसमता BOOK - MBD PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - बहुविकल्पी प्रश्न
6 Videos
- परिमेय संख्याएँ BOOK - MBD PUBLICATIONCHAPTER - परिमेय संख्याएँ EXERCISE - बहुविकल्पी प्रश्न (निम्नलिखित में प्रत्येक प्रश्न के उत्तर के लिए दिए है सही उत्तर का चयन कीजिए)
17 Videos
Similar Questions
निम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए : (π=227) लीजिये
14 cm
View Solution10 cm व्यास वाले एक वृत्त की परिधि ज्ञात कीजिए ? (π=3.14 प्रयोग कीजिए)
View Solutionनिम्न समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
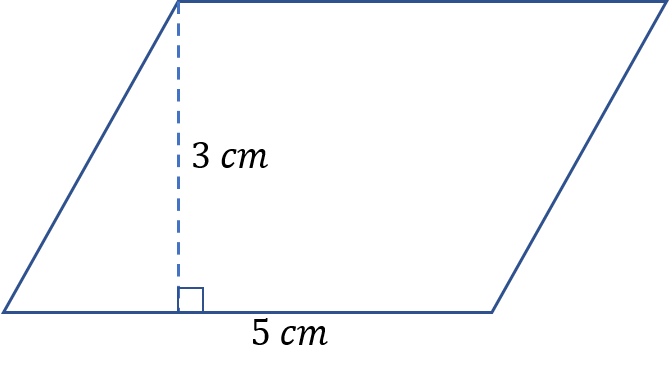
View Solutionनिम्न में से कौन सी वस्तुएँ सर्वांगसम हैं : -
View Solutionनिम्नलिखित में से कौन सी प्राकृत संख्या नहीं है?
View Solutionयदि 9 सेमी ऊँचाई वाले एक लंबवृत्तीय शंकु का आयतन 48π सेमी^(3) गहरा है, तो इसके आधार का व्यास ज्ञात कीजिए ?
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionसदिशों के प्रयोग द्वारा उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(2,3,5),B(3,5,8) और C(2,7,8) हैं |
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
View Solutionत्रिभुज का क्षेत्रफल ज्ञात करने का हीरोन का सूत्र लिखिए।
View Solutionकिसी त्रिभुज की ऊँचाई और आधार क्रमशः 8 cm व 3 cm हैं, उसका क्षेत्रफल होगा :
View Solutiontriangle ABC में, जिसका B कोण समकोण है, AB = 12 cm और BC = 5 cm है। sin C का मान है :
View Solution△ ABC में, जिसका कोण B समकोण है, AB = 5 cm और, BC = 12 cm है। cos C का मान है :
View Solution
