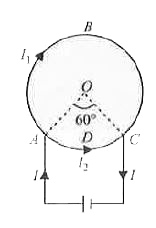
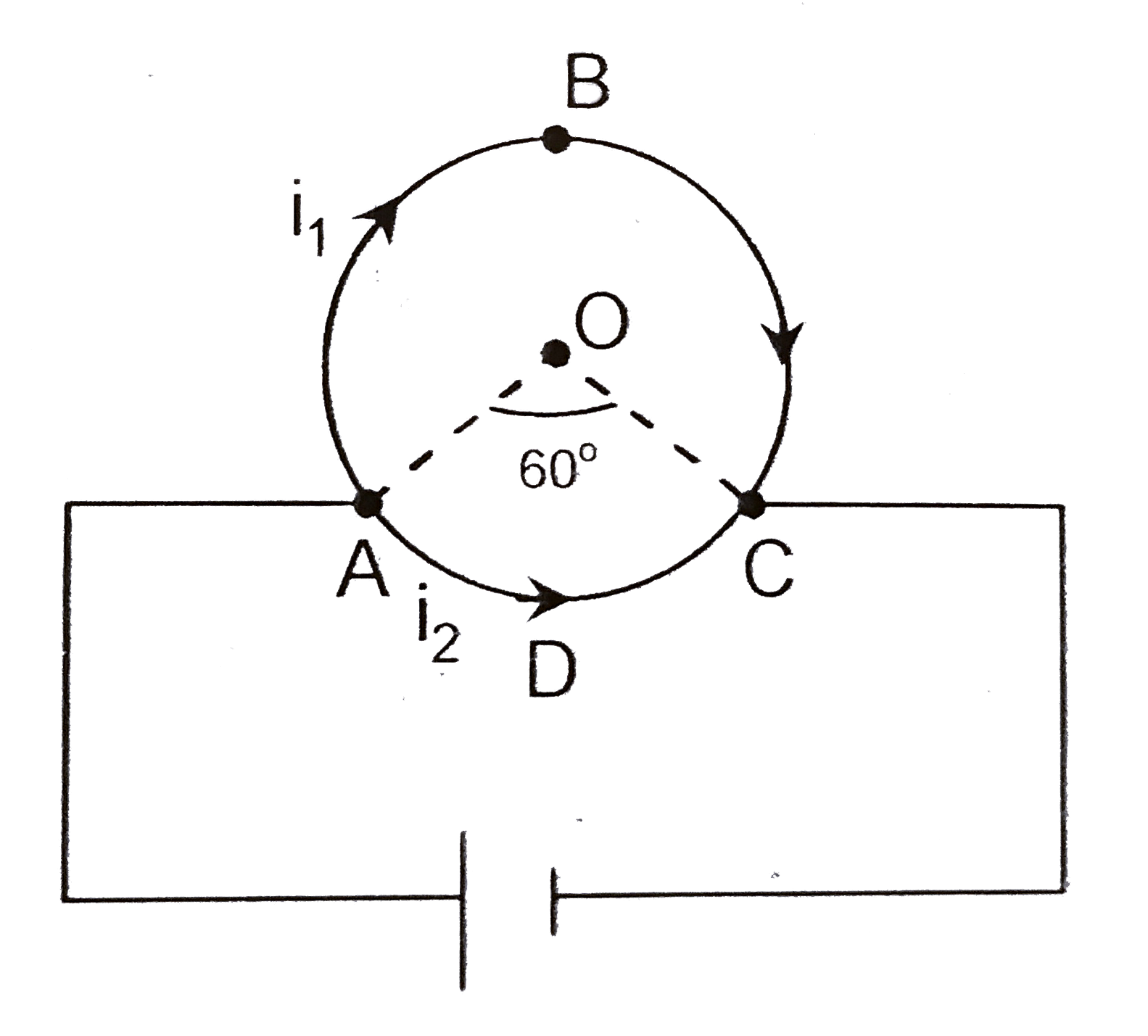
A cell is connected between the points A and Cofa circular conductor ABCDA of centre O. ∠AOC=60∘. If B1, and B2, are the magnitudes of the magnetic fields at O due to currents in ABC and ADC respectively, the ratio B1/B2, is
6
5
1
1/5
The correct Answer is:C
Let l1,l2 be the lengths of the two parts ABC and ADC of the lengths of the two parts ABC and ADC of the conductor and ρ be resistance per unit length of the conductor .
The resistance of the part ABC will be
R1=ρl2/A
The resistance of the part ABC will be
R2=ρl2/A
Potential difference across AC must be equal I1R1=I2ρl2
or I1ρl2/A=I2ρl2/A " "0r " " I1l1=I2l2
Magnetic field at O due to a cuttent I1 flowing in ABC is given by
B1=μ0I1θ14πr=μ0I1l14πr2 (Asl1=θ1r)
Magnetic field at O due to current I2 flowing in ADC is given by
B2=μ0I2θ24πr=μ0I2l24πr2 (Asl2=θ2r)
∴B1B2=1

Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(AMPER.S CIRCUITAL LAW AND ITS APPLICATIONS)
8 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(FORCE ON A MOVING CHARGE IN UNIFORM ELECTRIC AND MAGNETIC FIELDS)
37 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
Similar Questions
A cell is connected between the points A and C of a circular conductor ABCD of centre O .∠ AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is
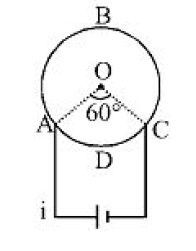
View SolutionA cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.∠AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is

View Solution
Knowledge Check
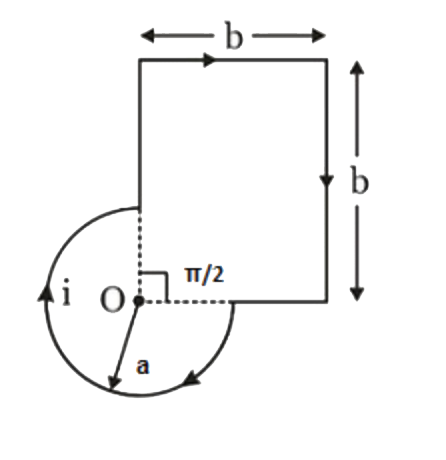
The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is
 AzeroBμ0(b−a)24abCμ0I4π[b−aab]Dμ0I4π[2(b−a)+π3(a+b)]
AzeroBμ0(b−a)24abCμ0I4π[b−aab]Dμ0I4π[2(b−a)+π3(a+b)]A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
AzeroBμ04π(I1−I2)Cμ02a(I1+I2)Dμ0a(I1+I2)The figure shows tow coaxial circulalr loop a1 and 2, which forms same solid angle θ at point O. If B1 and B2 are the magnetic fields produced at the point O due to loop 1 and 2 respectively, then
 AB1B2=1BB1B2=2CB1B2=8DB1B2=4
AB1B2=1BB1B2=2CB1B2=8DB1B2=4
A cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.∠AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is

View SolutionA cell is connected between the point A and C of a circular conductor ABCD of centre O,∠AOC=60∘. If B1 and B2 are the magnitude of magnetic fields at O due to the currents in ABC and ADC respectively, the ratio of B1/B2 is.
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
View SolutionThe figure shows tow coaxial circulalr loop a1 and 2, which forms same solid angle θ at point O. If B1 and B2 are the magnetic fields produced at the point O due to loop 1 and 2 respectively, then

View SolutionA and B are two concentric circular conductors of centre O and carrying currents i1 and i2 as shown in the adjacent figure. If ratio of their radii is 1:2 and ratio of the flux densities at O due to A and B is 1:3, then the value of i1/i2 is

View Solution
