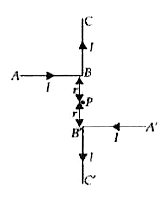
Current through ABC and A'B'C' is 1. What is the magneticfield at P? BP=PB=r(henceC'B'andpbc are collinear)

A

$B = \frac{1}{4 π} \frac{2 I}{r}$

B

$B = \frac{μ_{0}}{4 π} (\frac{2 I}{r})$

C

$B = \frac{μ_{0}}{4 π} (\frac{I}{r})$

D

zero

Text Solution

Verified by Experts

The correct Answer is:B

The magnetic field at point Pdue to current I in AB is
$B_{A B} = \frac{μ_{0}}{4 π} \frac{I}{r} \otimes$
The magnetic field at point P due to current I in BC is $B_{B C} = 0$
The magnetic field at point P due to current I in $A^{.} B^{.}$ is
$B_{A^{.} B^{.}}^{.} = \frac{μ_{0}}{4 π} \frac{I}{r} \otimes$
The magnetic field at point P due to current 1 in $B^{.} C^{.}$ is $B_{B^{.} C^{.}}^{.}$
$∴$ The net magnetic field at P is
$B = B_{A B} + B_{B C} + B_{A^{.} B^{.}}^{.} + B_{B^{.} C^{.}}^{.}$
$= \frac{μ_{0} I}{4 π r} + 0 + \frac{μ_{0} I}{4 π r} + 0 = 2 (\frac{μ_{0} I}{4 π r}) = \frac{μ_{0}}{4 π r} (\frac{2 I}{r})$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
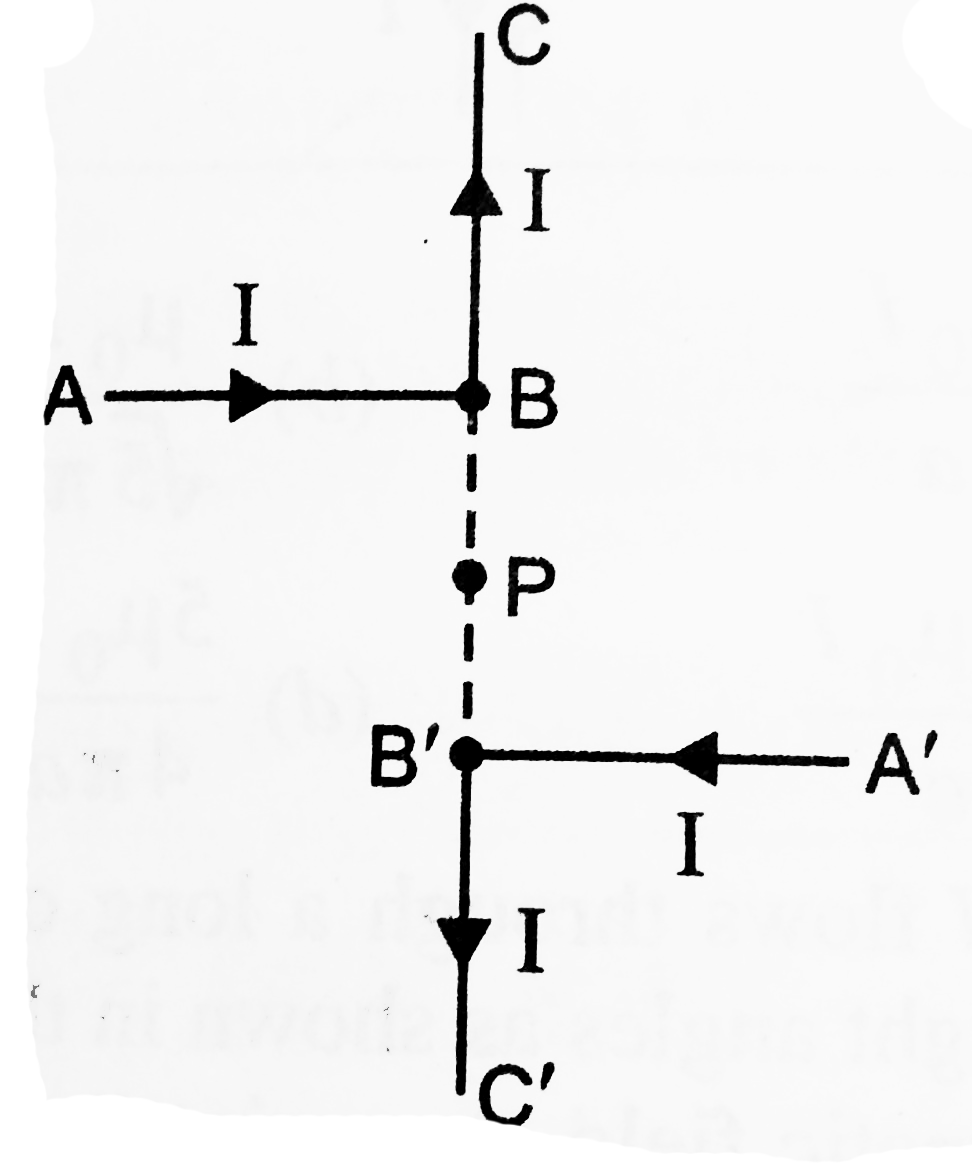
Current through ABC A'B'C' is I. What is the magnetic field at P? BP= PB' = r (Here C'B' PBC are collinear)

A $B = \frac{1}{4 π} \frac{2 I}{r}$
B $B = \frac{μ_{0}}{4 π} (\frac{2 I}{r})$
C $B = \frac{μ_{0}}{4 π} (\frac{I}{r})$
Dzero
Question 2 - Select One
Currents through ABC and $A^{'} B^{'} C^{'}$ is I, figure. What is the magnetic field at P? $B P = P B^{'} = r$ . (Here $C^{'} B^{'} P B C$ are collinear)

A $\frac{2 I}{4 π r}$
B $\frac{μ_{0}}{4 π} (\frac{2 I}{r})$
C $\frac{μ_{0}}{4 π} (\frac{1}{r})$
Dzero
Question 3 - Select One
A sphere of constant radius r through the origin intersects the coordinate axes in A, B and C What is the locus of the centroid of the triangle ABC?
A $x^{2} + y^{2} + z^{2} = r^{2}$
B $x^{2} + y^{2} + z^{2} = 4 r^{2}$
C $9 (x^{2} + y^{2} + z^{2}) = 4 r^{2}$
D $3 (x^{2} + y^{2} + z^{2}) = 2 r^{2}$

MTG GUIDE-MAGNETIC EFFECTS OF CURRENT AND MAGNETISM-NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(BIOT SAVART LAW AND ITS APPLICATIONS)

Home
Ask Doubt
Profile