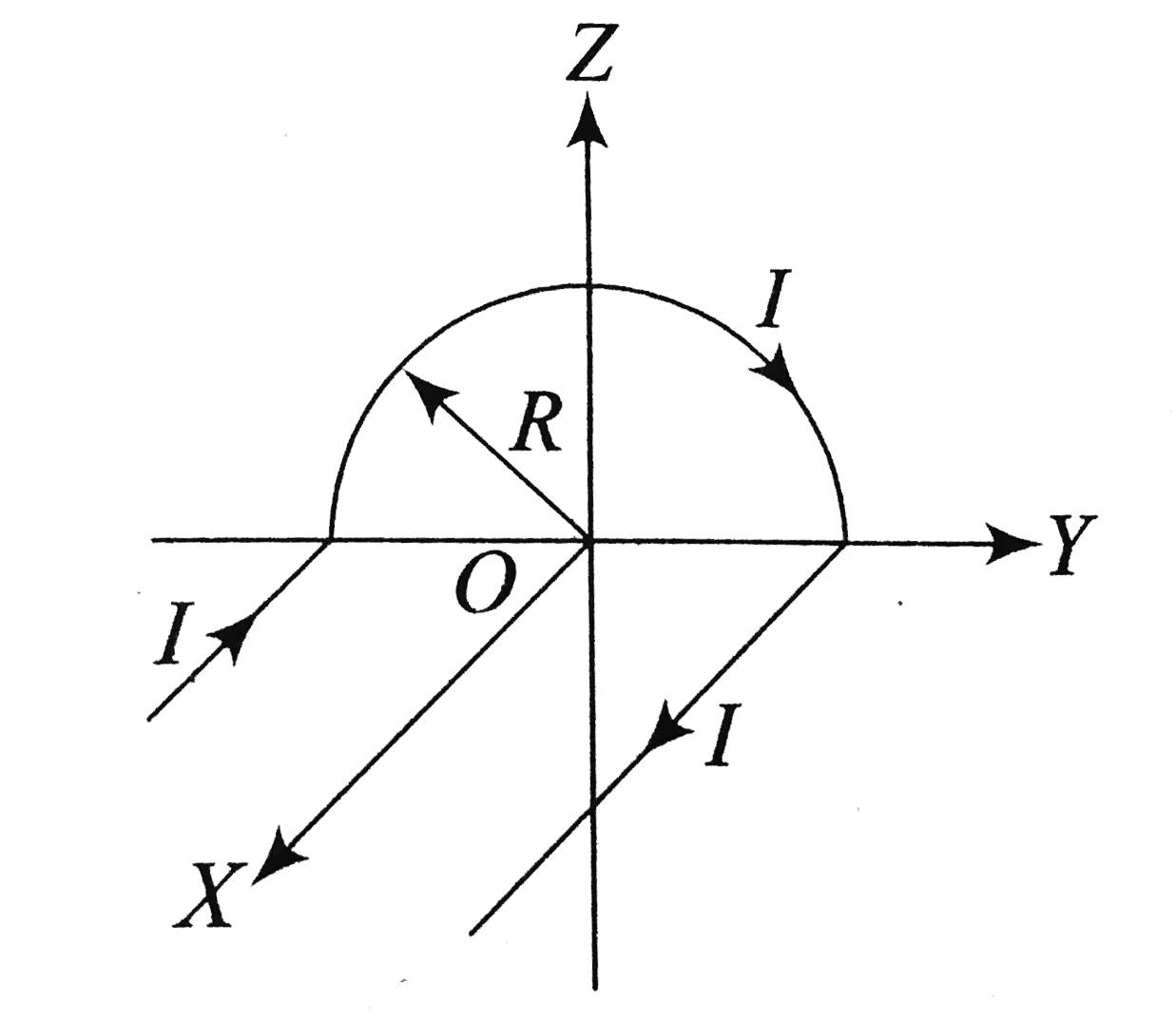
A wire carrying current I has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicircular portion of radius R is lying in Y-Z plane. Magnetic field at point O is
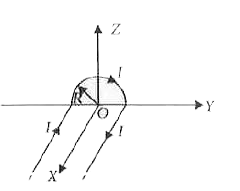
The correct Answer is:A
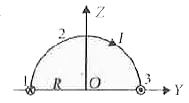
Given situation is shown in the figure. Parallel wires 1 and 3 are semi-infinite, so magneti field at O due to them
Magnetic field at O due to semi-circular arc in YZ-plane is given
Net magnetic field at piont O is given by
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - CHECK YOUR NEET VITALS
25 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
Similar Questions
A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
View Solution
Knowledge Check
A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
 A→B=μ04πIR(πˆi+2ˆk)B→B=−μ04πIR(πˆi−2ˆK)C→B=−μ04πIR(πˆi+2ˆk)D→B=μ04πIR(πˆi−2ˆK)
A→B=μ04πIR(πˆi+2ˆk)B→B=−μ04πIR(πˆi−2ˆK)C→B=−μ04πIR(πˆi+2ˆk)D→B=μ04πIR(πˆi−2ˆK)A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2A wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
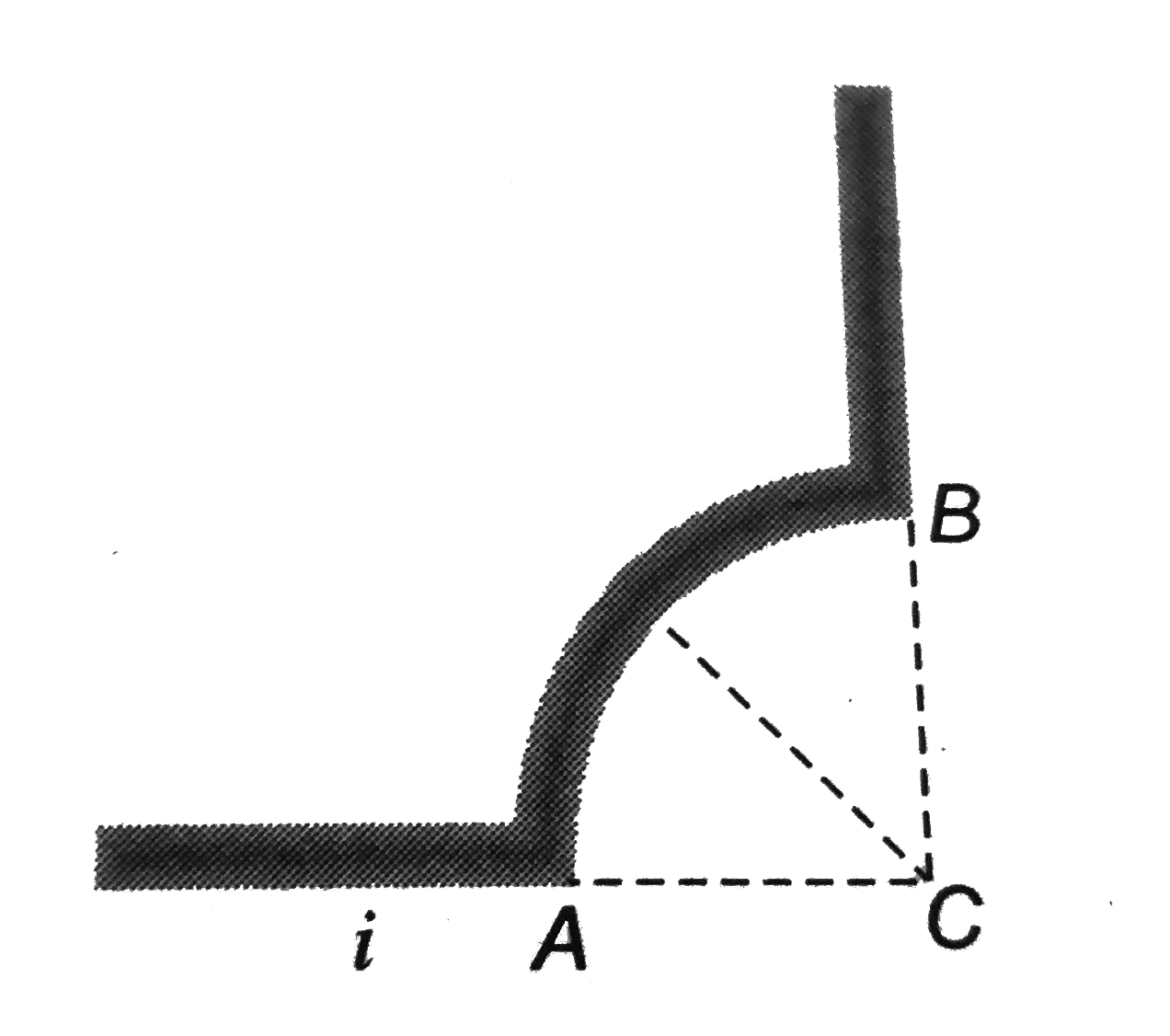 Aat an angle π4 to the plane of the paperBperpendicular to the plane of the paper and directed into the paperCalong the bisector of the angle ACB towards ABDalong the bisector of the angle ACB towards from AB
Aat an angle π4 to the plane of the paperBperpendicular to the plane of the paper and directed into the paperCalong the bisector of the angle ACB towards ABDalong the bisector of the angle ACB towards from AB
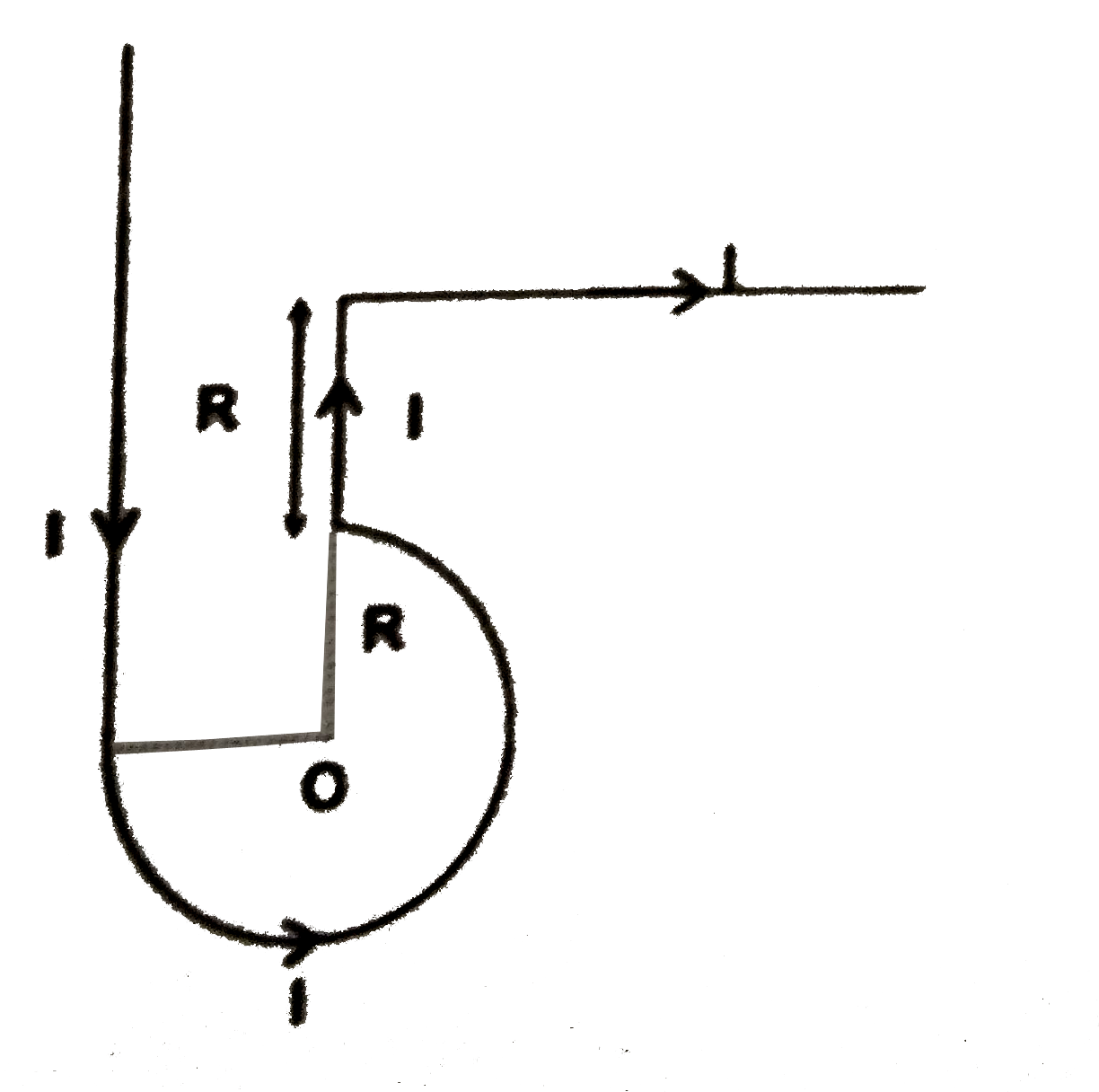
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
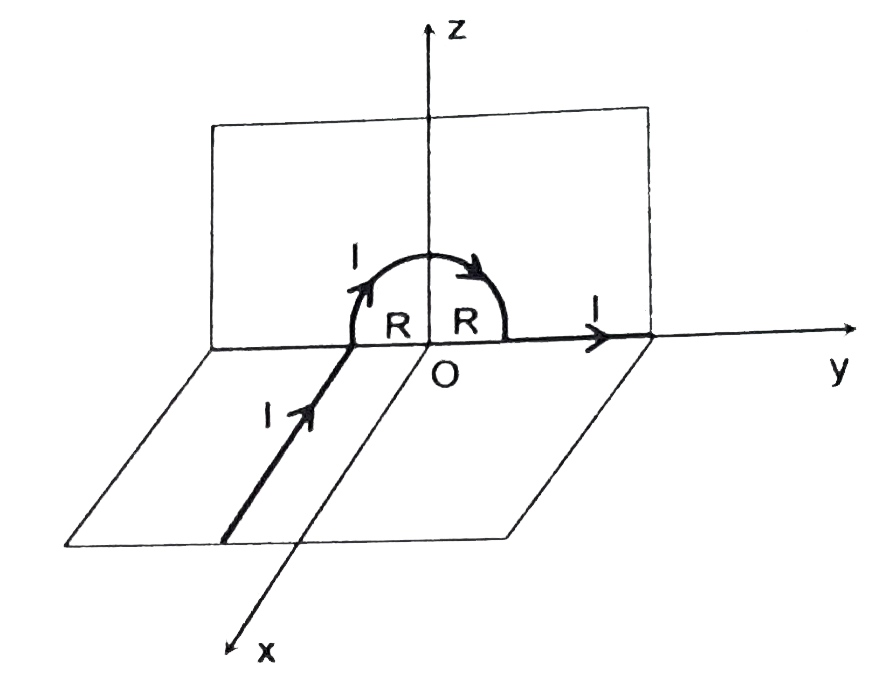
View Solution(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)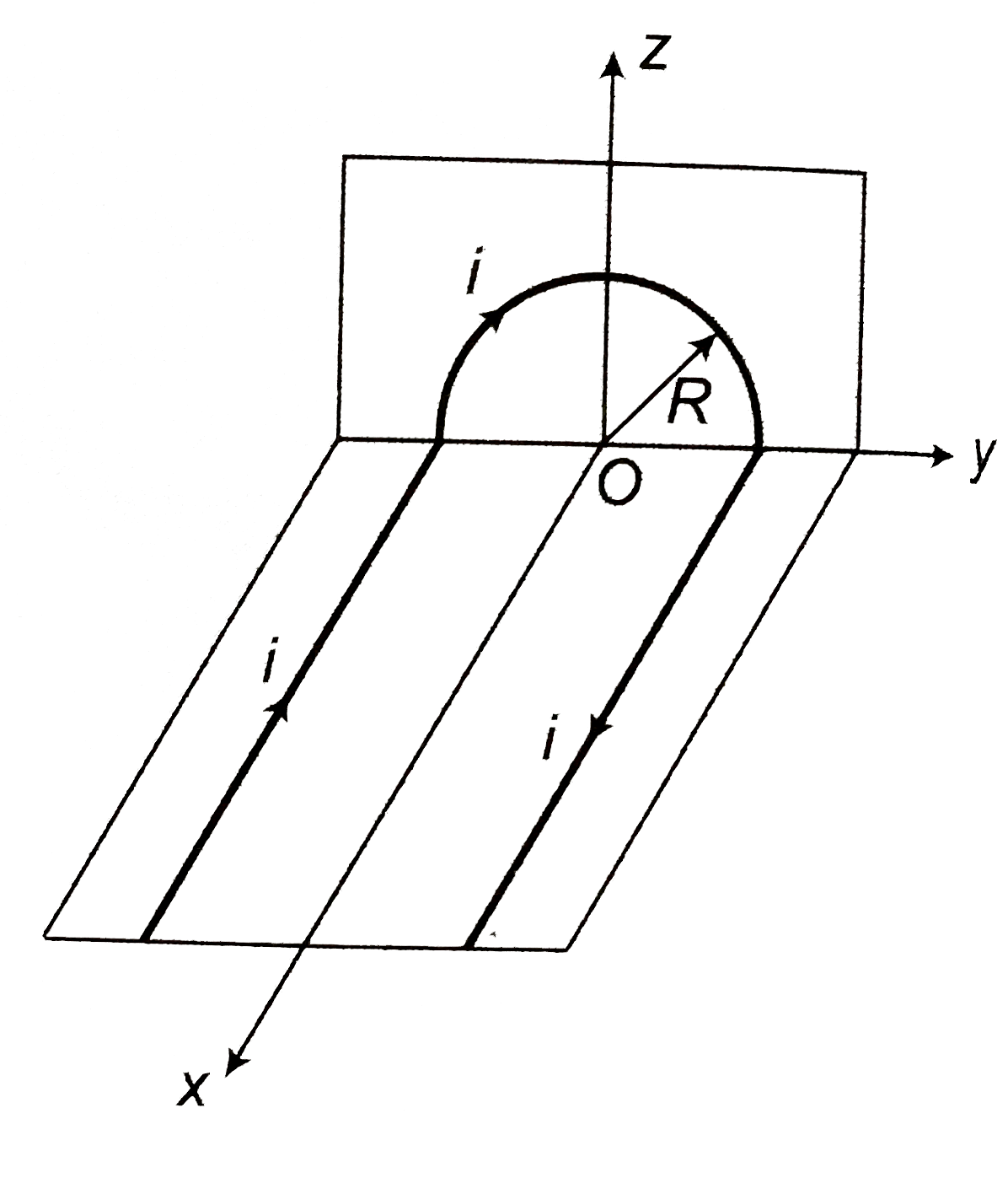
(ii)
(iii)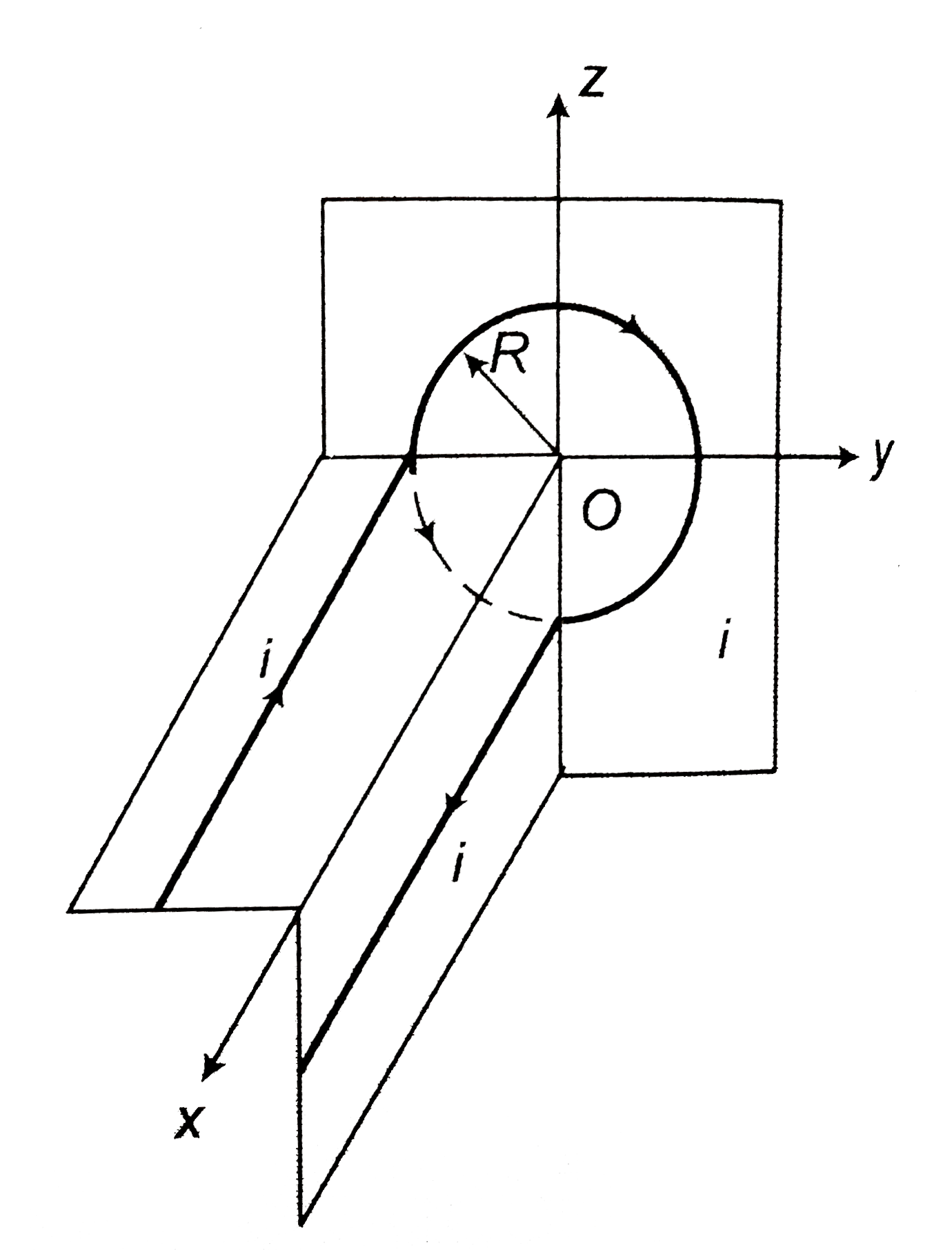
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
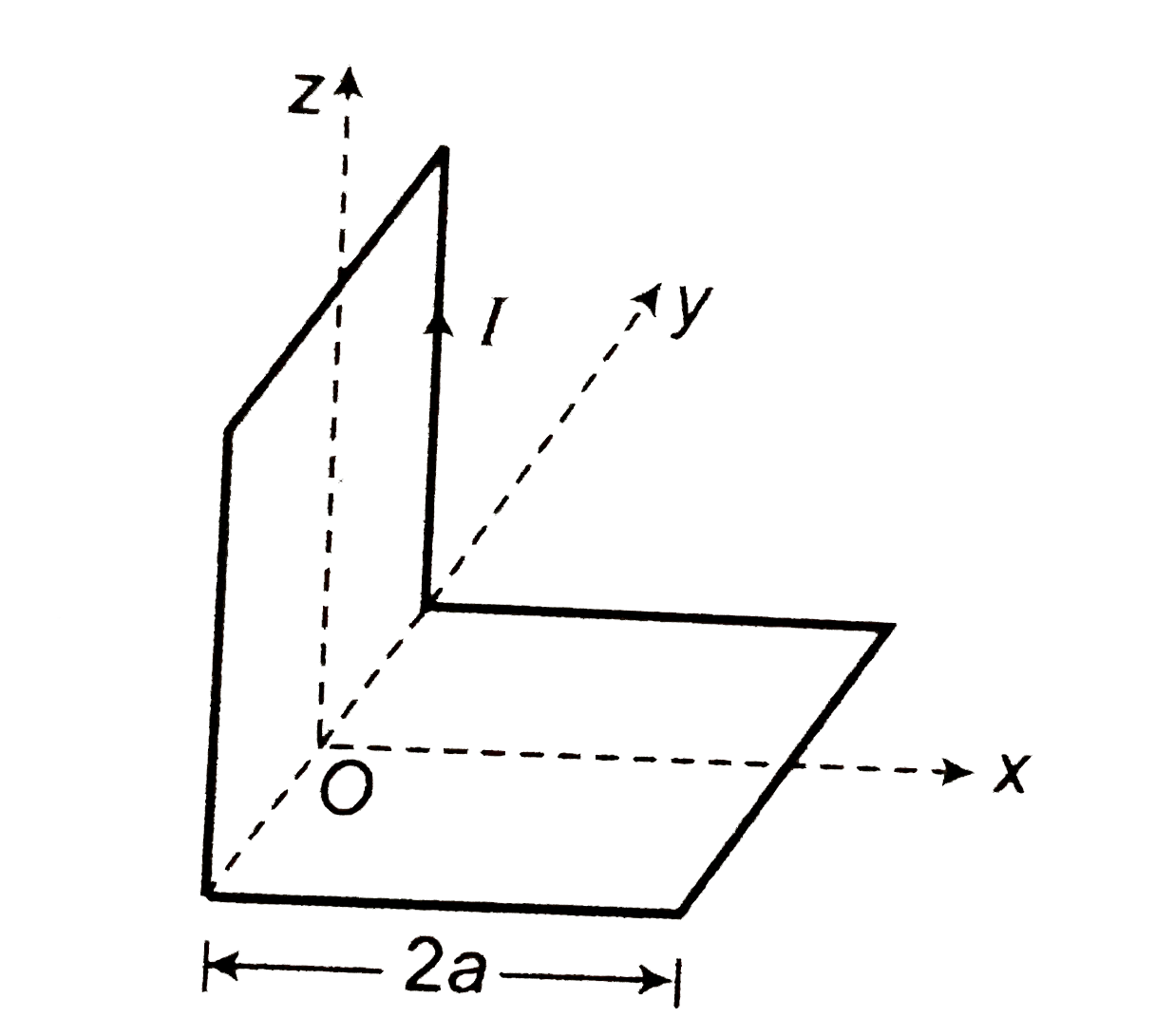
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View Solution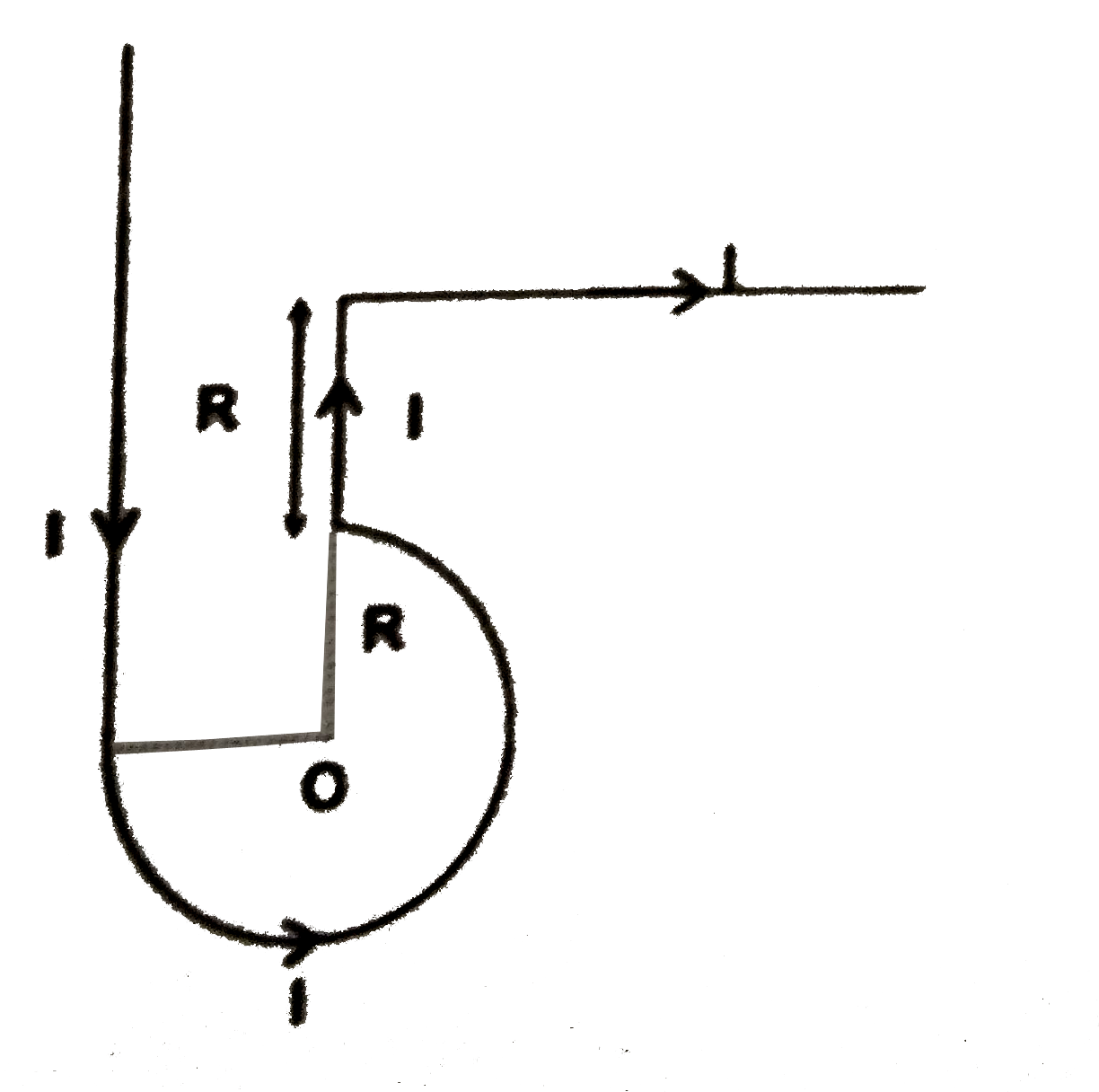
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View Solution
