In Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(ABC)=2 ar(BEC).Solution in Punjabi
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(ABC)=2 ar(BEC).Solution in Punjabi
Step by step video & image solution for In Fig. , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(ABC)=2 ar(BEC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
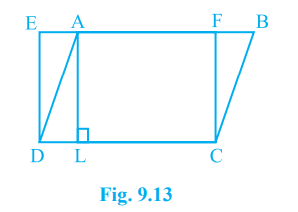
In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL
View SolutionGiven an arc of a circle, complete the circle.
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
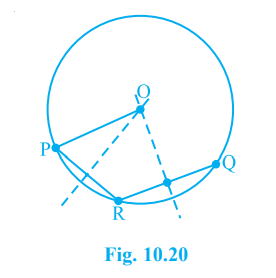
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View Solutionदिए गए आकृति में ABC और BDF दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य बिंदु है |यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाई की
ar(BDF)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE) ltBrgt (iii) ar(ABC)=2ar(BEC)
(iv) ar(BEF)=ar(AFD) ltBrgt (v) ar(BEF)=2ar(FED)
(vi)ar(FED)=18ar(AFC)
View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/4 ar( Delta ABC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/2 ar( Delta BAE)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta ABC) = 2 ar( Delta BEC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BFE) = 2 ar( Delta FED)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(BDE) = 1/4 ar(ABC)
View Solution
