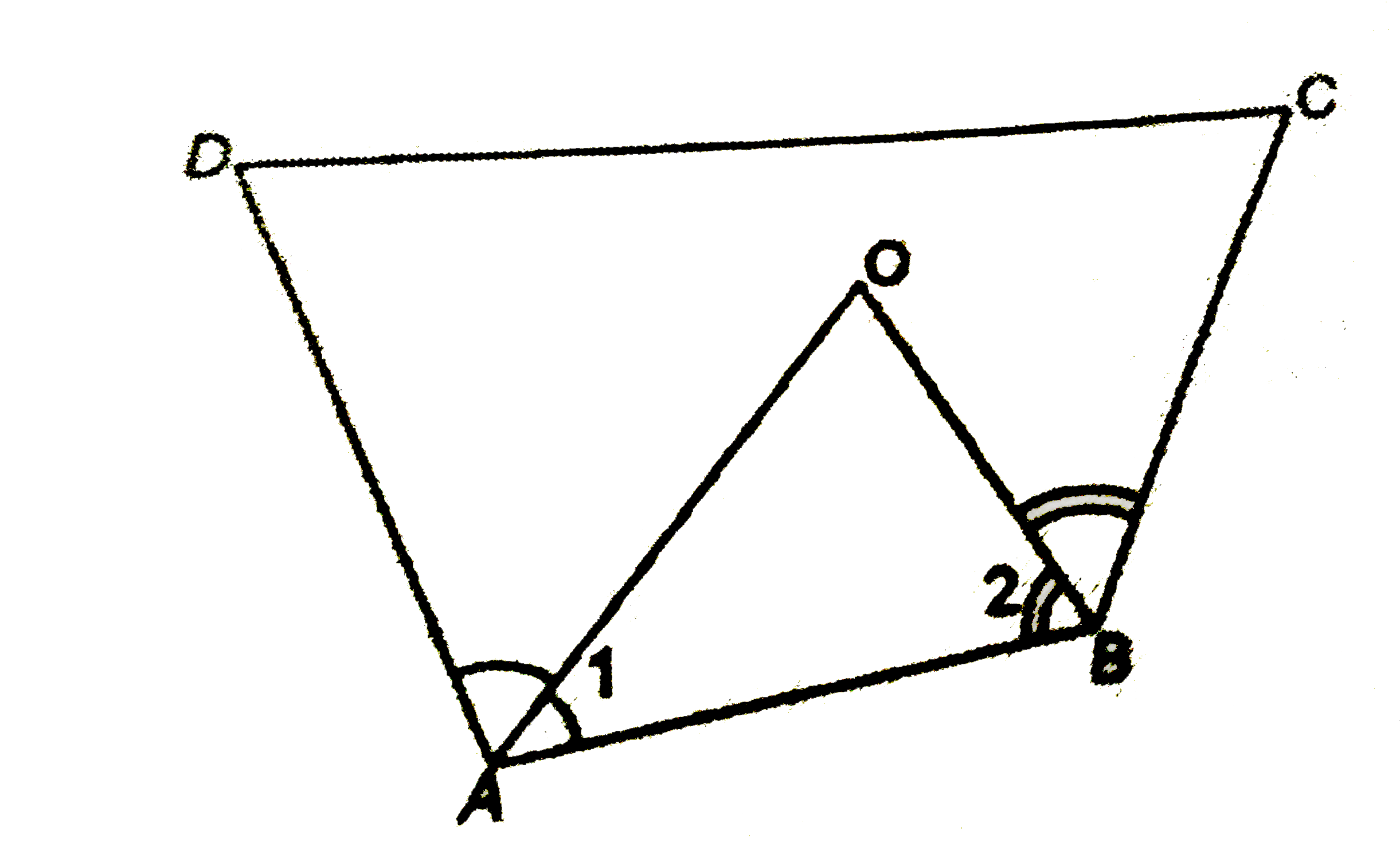
In quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
InΔΔOB+∠1+∠2=180∘
⇒ ∠AOB=180∘−(∠1+∠2)
⇒ ∠AOB=180∘−(∠A2+∠B2)
⇒ ∠AOB=180∘−12[360∘−(∠C+∠D)](∵∠A+∠B+∠C+∠D=360∘)
⇒ ∠AOB=180∘−180∘+12(∠C+∠D)
⇒ ∠AOB=12(∠C+∠D)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise12videos
STATISTICS
Similar Questions
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
View SolutionIn a quadrilateral ABCD,AO andBO are the bisectors of A∠ and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn a quadrilateral ABCD,AO andBO are the bisectors of A∠ and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn a quadrilateral ABCD,CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn a triangle ABC, ∠ABC= ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC=1200. Show that ∠A=∠B=∠C=600 .
View SolutionIn a parallelogram ABCD, the bisectors of ∠A and ∠B meet at O. Find ∠AOB.
View SolutionIn a ABC, AD bisects ∠A and ∠C>∠B. Prove that ∠ADB> ∠ADC .
View Solution

