ABCD is a parallelogram and AE and CF bisect ∠Aand∠C respectively. Prove that AE||FC.

Step by step video & image solution for ABCD is a parallelogram and AE and CF bisect angleA and angleC respectively. Prove that AE"||"FC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionABCD is a parallelogram in which ∠DAB=80∘. Bisector of ∠Aand∠B meets CD at P. Prove that :
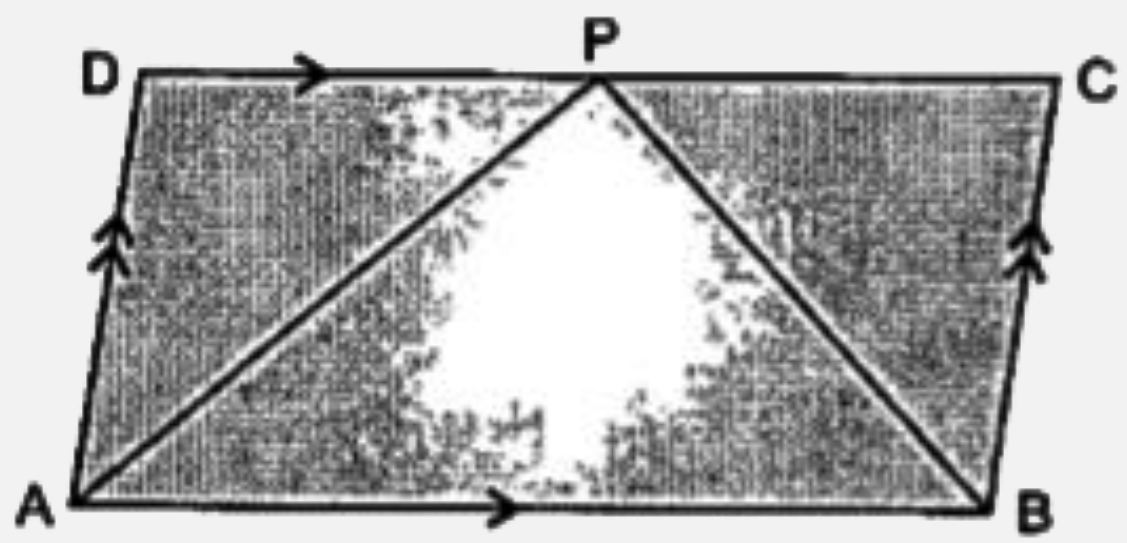
(i) AD = DP
(ii) CP = CB
(iii) DC = 2AD
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

∠DEC=90∘
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
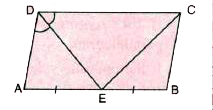
CE bisects angle C
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
View SolutionIn a parallelogram ABCD, ∠BCD=60∘ If the bisectors AP and BP of ∠Aand∠B respectively, meet the side CD at point P, then prove that CP = PD.
View Solution
