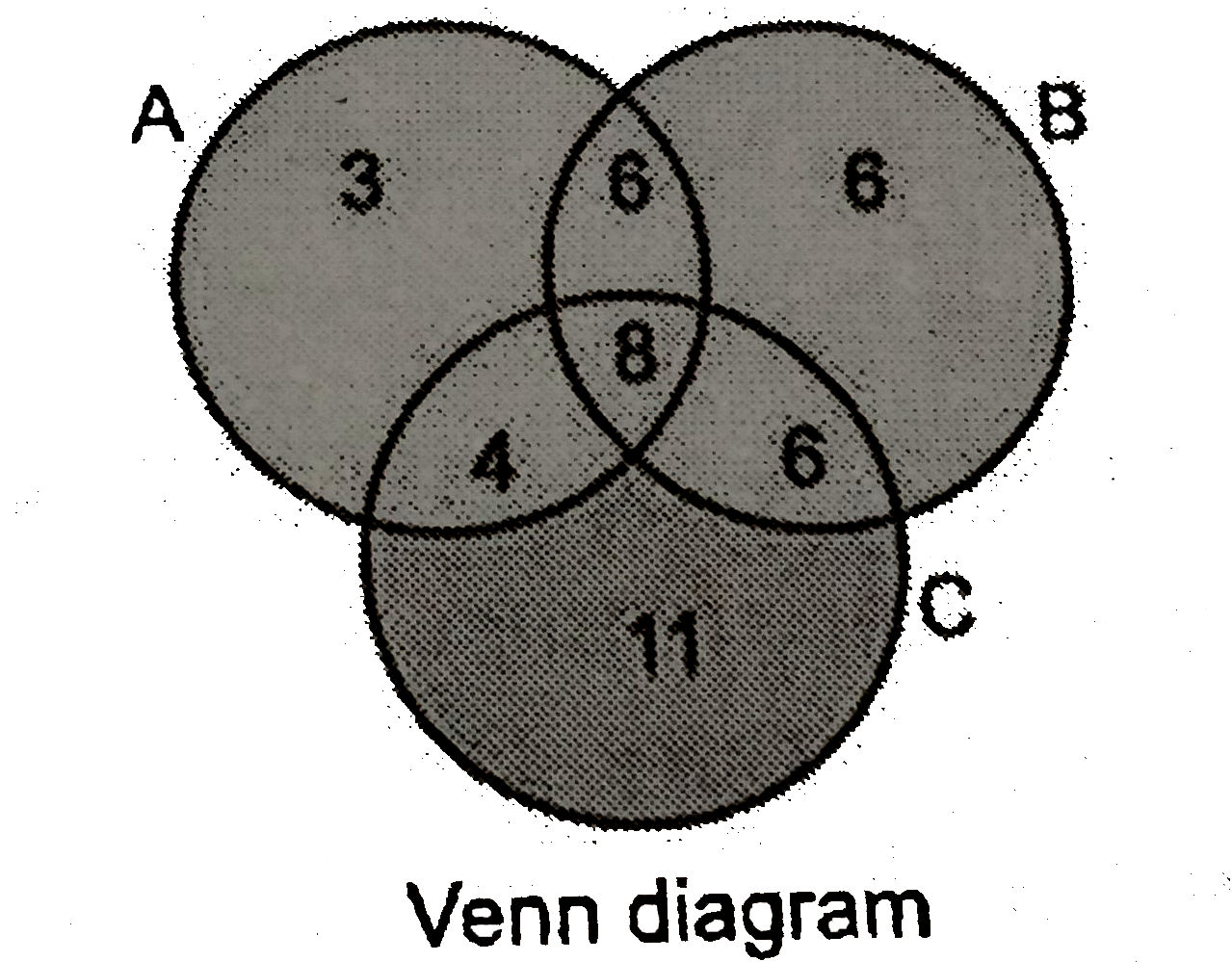
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked products C only?
Video Solution
Text Solution
n(A)=21andn(B)=26
Number of people who like product A and B both
n(A∪B)=n(A)+n(B)−n(A∩B)
=21+26−14=33
Now n(C)=29
Number of people who like product B and C both
n(B∩C)=14
Number of people who like product C and A both
n(A∩C)=12
Number of people who like product A,B and C, all
n(A∩B∩C)=8
Then, number of people who like any one of the one product
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)
−n(B∩C)−n(A∩C)+n(A∩B∩C)
=21+26+29−14−14−12+8
=44
∵n(A∪B∪C)=44andn(A∪B)=33
Number of people who like only product C
=n(A∪B∪C)−n(A∪B)=44−33=11
Therefore, number of people who like only product
C=11.
|
Topper's Solved these Questions
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1.6
8 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
Similar Questions
In a survery, it was found that 21 persons liked product A, 26 liked product B and 29 liked product C. If 14 persons liked products A and B, 12 liked products C and A, 13 persons liked products B and C and 8 liked all the three products then
(i) Find the number of persons who liked the product C only
(ii) The number of persons who like the products A and B but not C
View Solution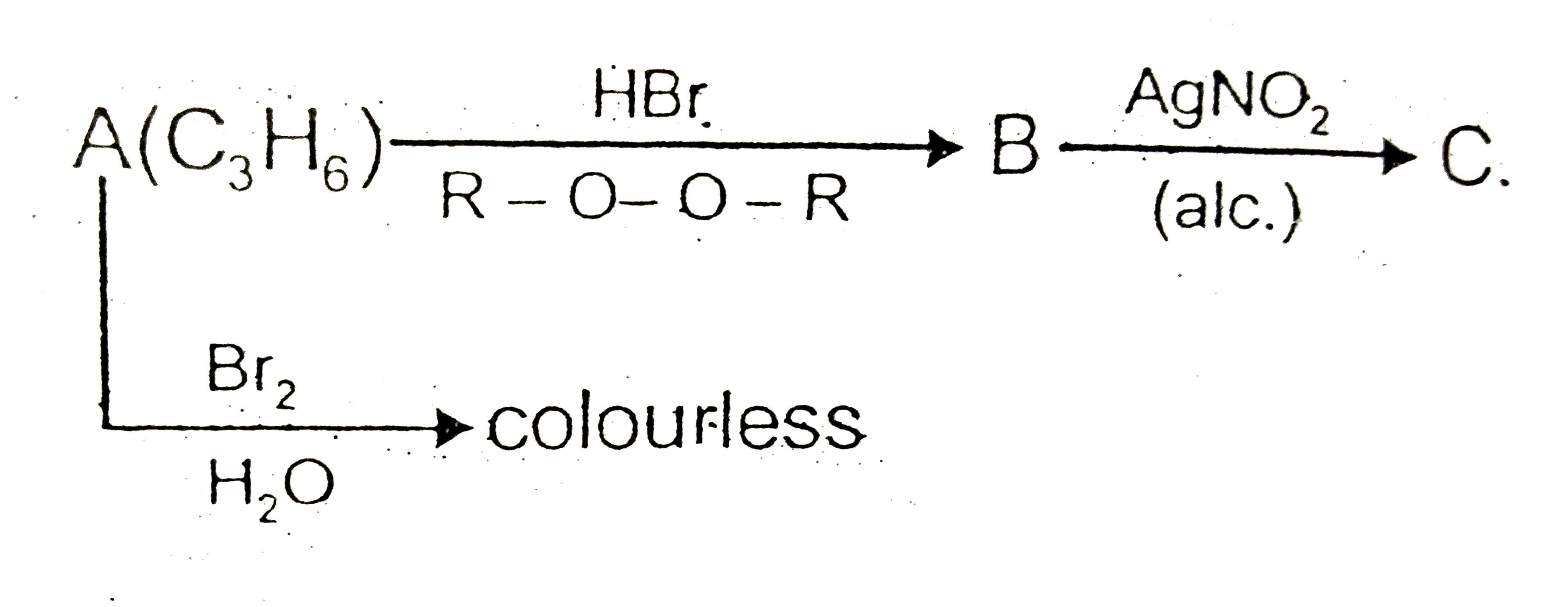
The product C is
View Solution
Knowledge Check
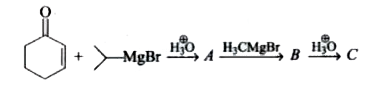
Product A and C are:A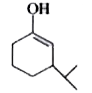 B
B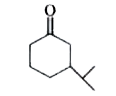 C
C D
D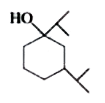

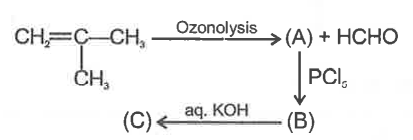 The product "C" is
The product "C" is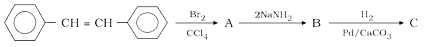 The product (C) is :
The product (C) is : . The product C is
. The product C is