In the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

(i) In ΔABD and ΔACE,
∵⎧⎪⎨⎪⎩∠3=∠3(common)∠1=∠2(each 90∘, given)BD=CE(given)
∴ΔABD≅ΔACE (AAS) Hence Proved.
(ii) AB=AC (c.p.c.t)
Hence, ΔABC is an isosceles triangle. Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
In the adjoining figure, ∠BAC=∠BDC and ∠ABC=∠BCD. Prove that :
(i) ΔABC≅ΔDCB
(ii) ΔABE≅ΔDCF.

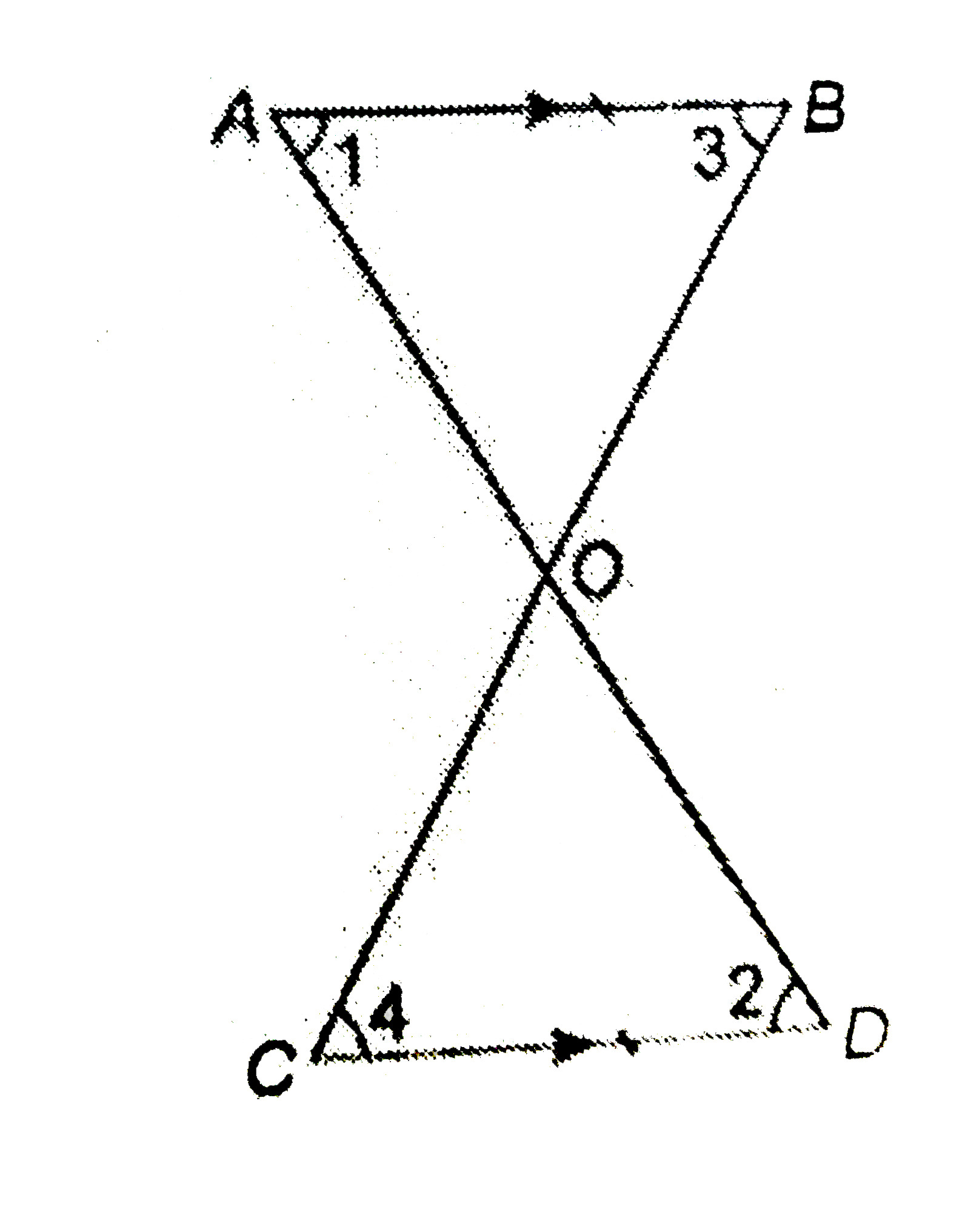
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
View SolutionIn the adjoining figure, AD=DC and DB bisects ∠ADC. Prove that ΔADB≅ΔCDB.

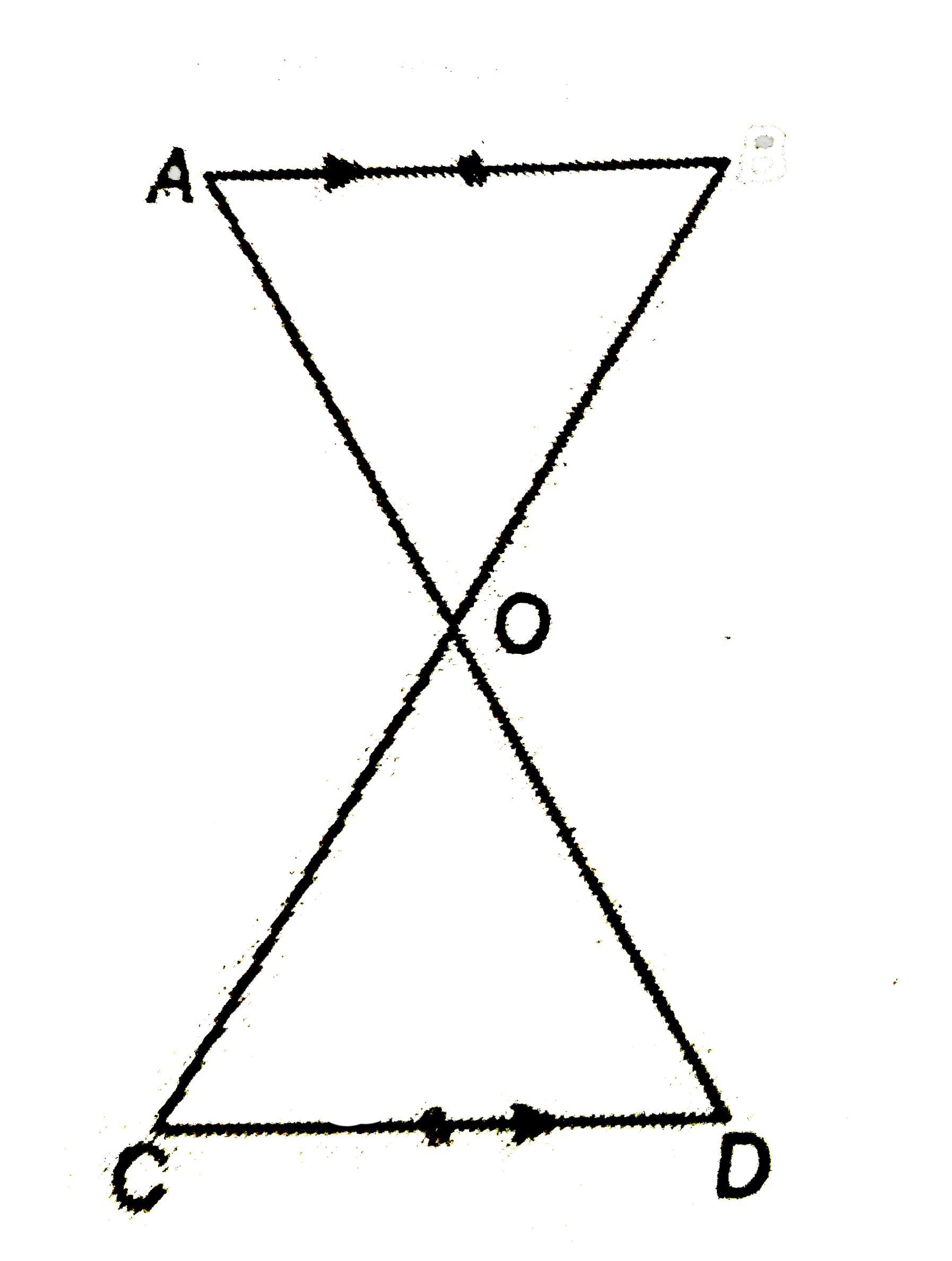
View SolutionIn the adjoining figure AB=CD and AB||CD prove that :
(i) ΔAOB≅ΔDOG
(ii) AD and BC bisect each other at point O.
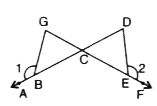
View SolutionIn the given figure , BC = CE and ∠1=∠2.
Prove that :
ΔGCB=ΔDCB .
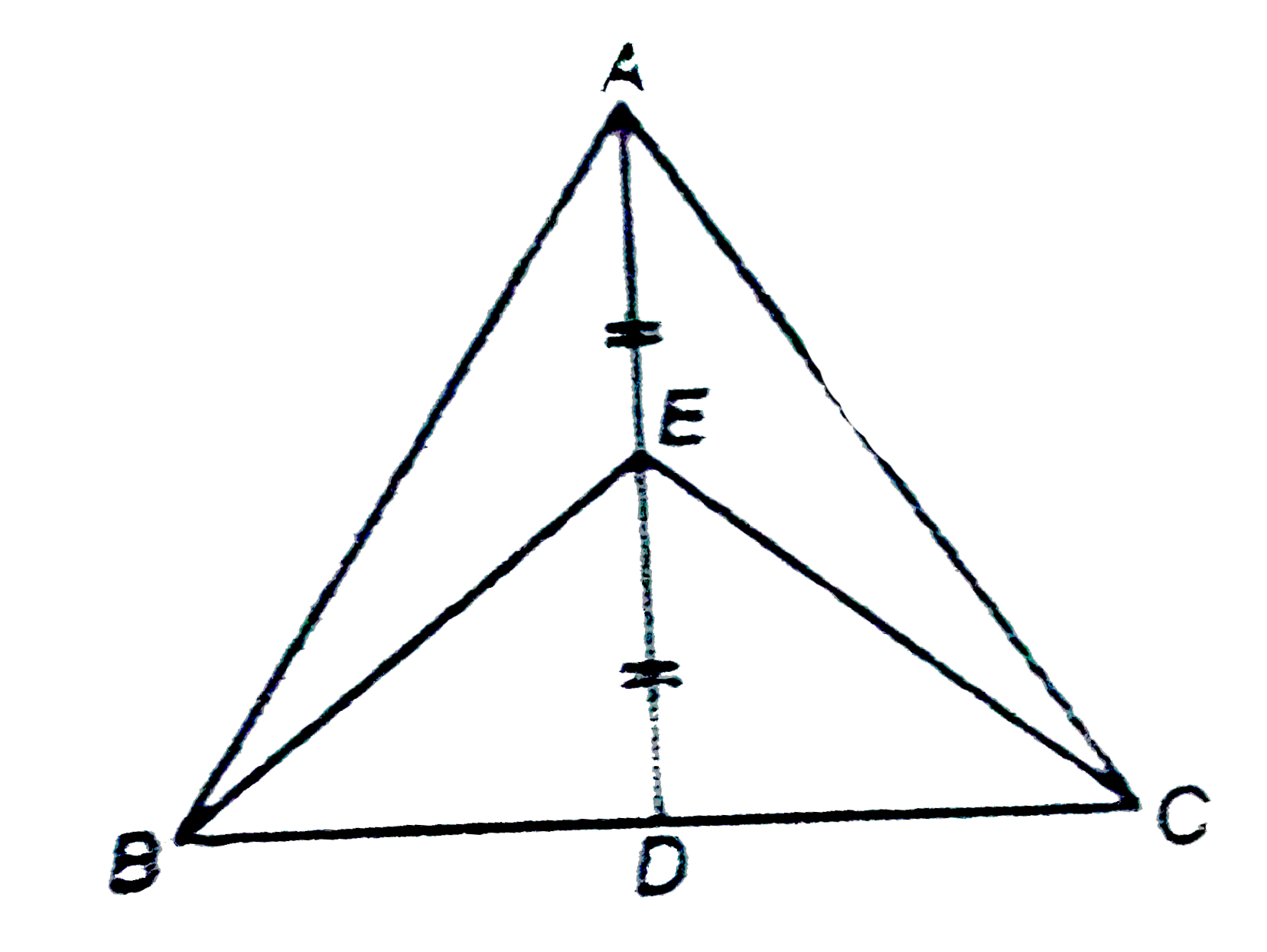
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
View SolutionIn the adjoining figure, AB= AD, BD= CD and ∠DBC=2∠ABD
Prove that : ABCD is a cyclic quadrilateral.

View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.
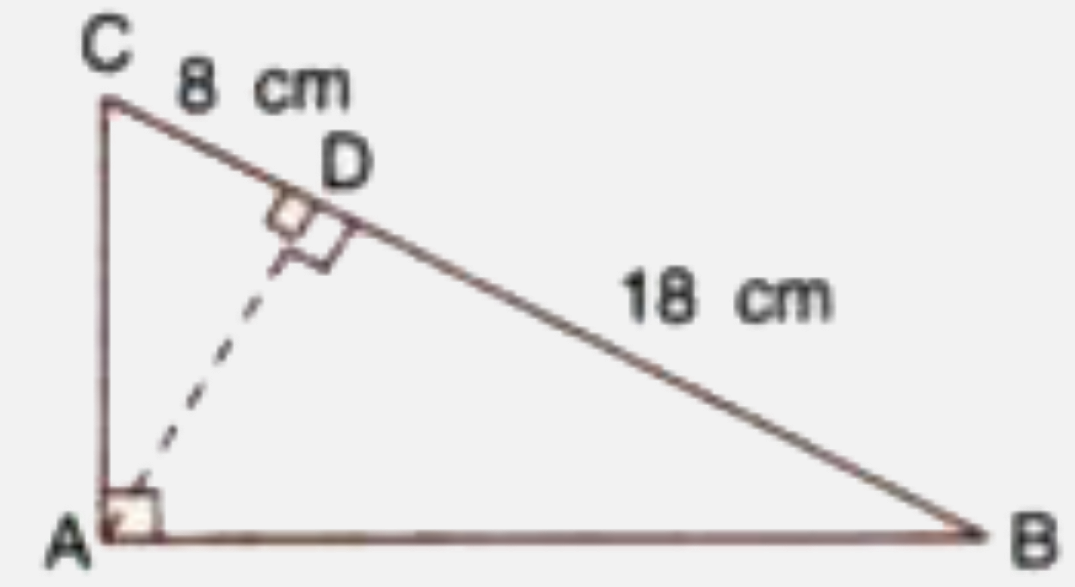
Prove that : ΔADB~ΔCDA.
View SolutionIn the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQand∠PAC. If ∠BAQ=30∘, prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle

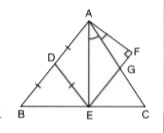
View SolutionIn the given figure, AD = DB = DE ∠EAC=∠FACand∠F=90∘
Prove that
(i) ∠AEB=90∘
(ii) ΔCEG is isosceles.
(iii) ∠CEG=∠EAF
View Solution
